풀이
[문제 풀이]
이 문제를 처음 봤을 때 이전에 풀었던 숫자 타자 대회와 비슷하다는 느낌을 받았다.
다른 점은 w가 1000으로 컸기 때문에 문제의 시간복잡도가 O(n^2)인지 아닌지 고민을 많이했다.
고민해본 결과 다행히 시간복잡도 O(n^2)으로 풀 수 있다는 생각이 들었고, 아이디어를 구현했다.
아이디어는 다음과 같다.
2차원 배열 DP[A][B]를 만들고 1번째 경찰차가 A 위치에 있으며, 2번째 경찰차가 B 위치에 있는 경우에 이동거리의 최소값으로 정의한다.
이렇게 정의할 경우 i번째 사건이 일어났을 경우 1번 경찰차와 2번 경찰차 중 하나는 반드시 i-1번째 위치에 있어야 하기 때문에 경찰차의 위치의 조합이 n^2이 아니라 2*n으로 나오게 된다. (조합이 2*n이라 시간 복잡도가 O(n^2)이 된다.)
좀 더 이해가 쉽도록 그림으로 생각해 보자
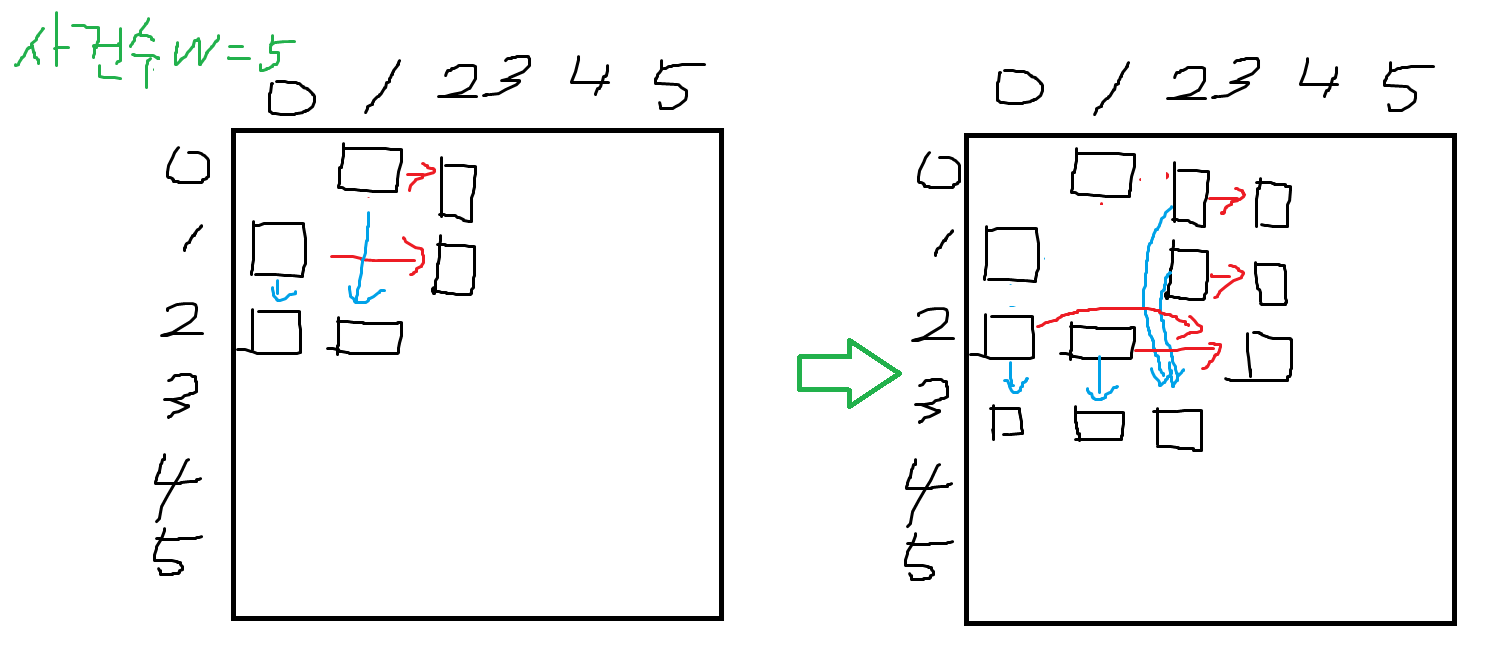
위 그림은 사건 w가 5개인 경우다.
왼쪽 그림은 사건이 2개인 경우에 각 값들을 저장한 모습이고 오른쪽 그림은 사건이 3개로 늘어난 경우다.
3개로 늘어난 경우 (3, 0)의 최소 이동거리를 구하는 방법은 하나다. (2, 0)에 위치하던 경찰차가 이동하는 경우다.
왜냐하면 2번 경찰차가 1의 사건으로 이동할 경우 0으로 갈 수 없기 때문이다.
마찬가지로 (3, 1)의 최소 이동거리도 (2, 1)에서 (3, 1)로 이동하는 경우 밖에 없다.
최소 이동거리를 고려해야하는 경우는 두 경우 밖에 없다.
바로 (2, 3)과 (3, 2)에 위치하는 경우다.
(2, 3)로 이동할 수 있는 경우는 [(2, 0), (2, 1)]의 값을 비교해야한다.
0번 자리에 있던 2번째 경찰차가 이동하거나, 1번 자리에 있던 2번째 경찰차가 이동해 (2, 3)에 위치할 수 있기 때문이다.
(3, 2)의 경찰차도 마찬가지다.
(여기서 경찰차 2대가 한 사건을 맡는 일은 없으므로 (2, 2)는 고려 x)
이유를 잘 생각해보면 항상 i번째 사건 전에 하나의 경찰차는 i-1번째 사건을 맡았다.
여기서 i번째 사건도 i-1번째 사건을 맡았던 경찰차가 맡는다면 다른 경찰차는 원래 위치에 그대로 있으므로 다른 경우를 고려할 필요가 없다.
하지만 i번째 사건을 i-1번째 사건을 맡은 경찰차가 이동하지 않는 경우는 다른 경찰차가 (0 ~ i-2)번째 사건을 맡는 경우들이 있으므로 여러 경우를 비교해 최소값을 저장하는 것이다.
이렇게 DP로 최소 이동거리를 구했다면, 몇 번째 사건을 어느 경찰차가 맡았는지 구해야한다.
나는 최소값을 저장할 때 이전에 경찰차들이 어느 위치에 있는지 저장했다.
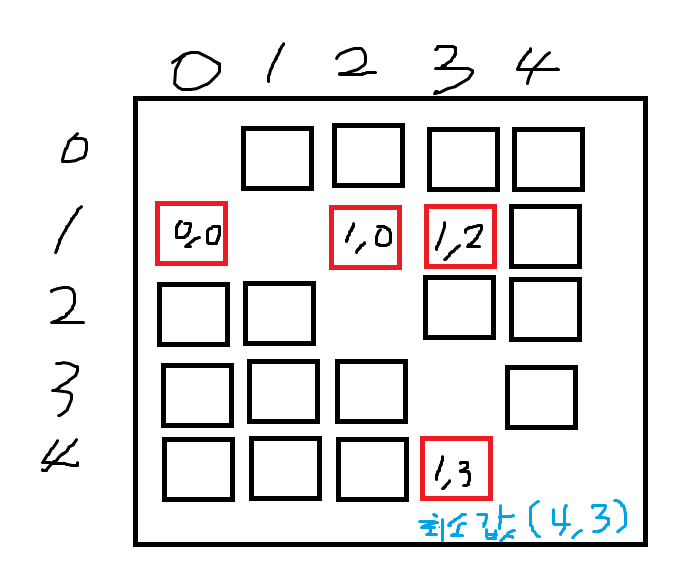
만약 위 그림처럼 (4, 3) 위치가 이동거리의 최소값이라면, 경찰차들이 이전에 어떤 사건을 맡았는지를 이용해 구할 수 있다.
1. (4, 3)에서 앞에 있는 4가 더 크므로 4번째 사건은 1번 경찰차가 맡는다.
2. (1, 3)위치로 이동하고 뒤의 3이 더 크므로 3번째 사건은 2번 경찰차가 맡는다.
3. (1, 2)위치로 이동하고 뒤의 2가 더 크므로 2번째 사건은 2번 경찰차가 맡는다.
4. (1, 0)위치로 이동하고 앞의 1이 더 크므로 1번째 사건은 1번 경찰차가 맡는다.
5. 초기 위치인 (0, 0)이므로 탐색을 종료한다.
이렇게 탐색을 통해 어떤 경찰차가 사건을 맡았는지 구할 수 있다.
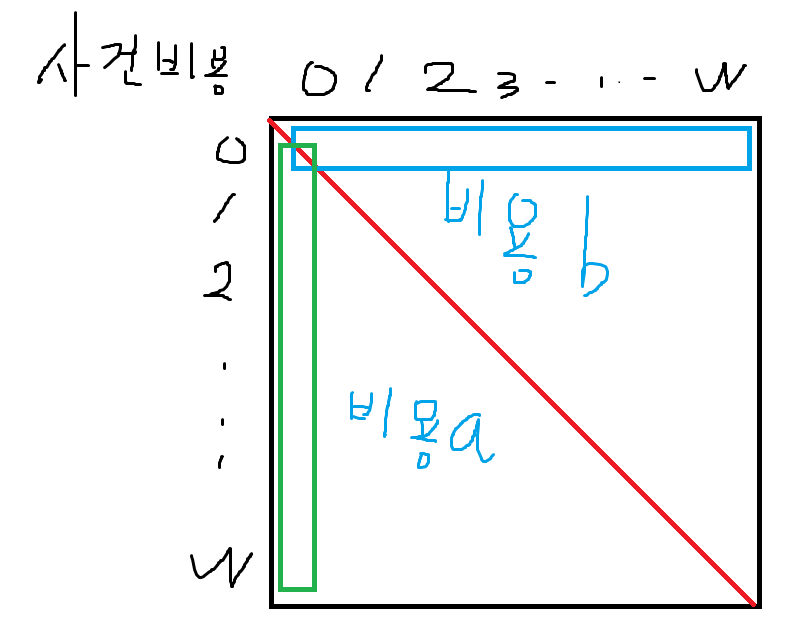
+ 추가로 이동 비용을 미리 계산할 때, 2번 경찰차의 초기 위치는 (n, n)이므로 a번 경찰차가 이동하는 경우, b경찰차가 이동하는 경우를 아래 그림과 같이 구분했다. (초록, 파랑 부분만 비용이 다름)
[아이디어 정리]
- DP[A][B]를 1번 경찰차가 A위치에 있는 경우, 2번 경찰차가 B위치에 있는 경우로 정의한다.
- i번째 사건이 일어난 경우 이전 사건에서 적어도 한 경찰차는 i-1번째에 위치해 있다는 사실을 이용한다.
- DP에서 최소 이동거리를 구하면서 이전에 경찰차가 어디에 위치했는지 저장한다.
- 최소 이동거리의 계산이 끝났다면, 이전 경찰차의 위치를 이용해 i번째 사건을 어떤 경찰차가 맡았는지 계산한다.
- 최소 이동거리와 각 사건을 맡은 경찰차를 출력한다.
Code
#include <iostream>
#include <vector>
#include <string>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int n, w;
cin >> n >> w;
vector<pair<int, int>> event(w + 1);
vector<vector<int>> cost(w + 1, vector<int>(w + 1, 0)); //0은 절반씩 사용 //a는 [출발지][도착지] b는 [도착지][출발지]
int a, b;
for (int i = 1; i <= w; i++)
{
cin >> a >> b;
event[i] = make_pair(a, b);
}
int nC;
for (int i = 1; i <= w; i++)
{
nC = abs(event[i].first - 1) + abs(event[i].second - 1);
cost[0][i] = nC; //a의 이동비용
nC = abs(event[i].first - n) + abs(event[i].second - n);
cost[i][0] = nC; //b의 이동비용
for (int j = i + 1; j <= w; j++)
{
nC = abs(event[i].first - event[j].first) + abs(event[i].second - event[j].second);
cost[i][j] = nC, cost[j][i] = nC;
}
}
vector<vector<int>> abCost(w + 1, vector<int>(w + 1, 0)); //[i][j] i == a의위치 j ==b의 위치
vector<vector<pair<int, int>>> abPair(w + 1, vector<pair<int, int>>(w + 1)); //[i][j] i == a의위치 j ==b의 위치
for (int i = 1; i <= w; i++)
{
abCost[i - 1][i] = abCost[i - 1][0] + cost[i][0]; // b가 0위치에서 i로 이동하는 경우
abPair[i - 1][i] = make_pair(i - 1, 0);
abCost[i][i - 1] = abCost[0][i - 1] + cost[0][i]; // a가 이동하는 경우
abPair[i][i-1] = make_pair(0, i - 1);
//a는 [출발지][도착지] b는 [도착지][출발지]
for (int j = 0; j < i; j++)
{
if (i - 1 == j) {
continue;
}
if (abCost[i][i - 1] > abCost[j][i - 1] + cost[j][i])
{
abCost[i][i - 1] = abCost[j][i - 1] + cost[j][i];
abPair[i][i-1] = make_pair(j, i - 1);
}
if (abCost[i - 1][i] > abCost[i - 1][j] + cost[i][j]) //b가 j에서 i로 이동하는 것
{
abCost[i - 1][i] = abCost[i - 1][j] + cost[i][j];
abPair[i - 1][i] = make_pair(i - 1, j);
}
// a가 이동하는 경우
abCost[i][j] = abCost[i - 1][j] + cost[i - 1][i];
abPair[i][j] = make_pair(i - 1, j);
// b가 이동하는 경우
abCost[j][i] = abCost[j][i-1] + cost[i][i-1]; //b가 i-1에서 i로 이동하는 것
abPair[j][i] = make_pair(j,i-1);
}
}
int minCost = 1000000000;
for (int i=0; i<w; i++)
{
if (abCost[i][w] < minCost) {
minCost = abCost[i][w];
a = i, b = w;
}
if (abCost[w][i] < minCost) {
minCost = abCost[w][i];
a = w, b = i;
}
}
cout << minCost <<"\n";
pair<int, int>np;
vector<int> ans(w + 1, 0);
if (a == w) {
ans[w] = 1;
}
else {
ans[w] = 2;
}
while (a!=0||b!=0)
{
if (a<b)
{
ans[b] = 2;
}
else
{
ans[a] = 1;
}
np = abPair[a][b];
a=np.first,b=np.second;
}
for (int i = 1; i <= w; i++) {
cout << ans[i] << "\n";
}
return 0;
}
아이디어는 빠르게 생각났는데, 생각보다 문제를 푸는데 오래걸렸다...
코드를 구현할 때 괜히 메모리를 많이 잡아먹는 것 같아서 줄이려다가 뻘짓을 하는 바람에 코드가 꼬여버렸기 때문이다...
덕분에 오류 투성이를 고친다고 이상한 데서 시간이 오래 걸리고 코드도 길어져버렸다 ㅠㅠㅠ
좀 더 깔끔하고 효율적인 코드로 풀고 싶었는데...
https://www.acmicpc.net/problem/2618
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 숨바꼭질 4 (0) | 2024.05.11 |
|---|---|
| [백준/C++] 조용히 하라고!! (0) | 2024.05.10 |
| [백준/C++] LCS 2 (0) | 2024.05.08 |
| [백준/C++] 가장 긴 증가하는 부분 수열 5 (0) | 2024.05.07 |
| [백준/C++] 냅색문제 (1) | 2024.05.05 |