풀이
[문제 풀이]
이 문제는 단순하게 모든 경우를 구하면 시간이 오래 걸리게 된다.
N이 30이기 때문에 부분집합의 모든 경우는 2^n이다.
여기서 Meet in the middle 이란 알고리즘을 이용하면 시간을 줄일 수 있다.
비슷한 문제로는 아래의 문제가 있다.
세 수의 합
MITM 알고리즘에 대해 간단히 설명하면 경우의 수가 매우 큰 상황에서 Bruteforce로 문제를 풀어야 할 경우 적절히 분할하면 연산의 수를 줄일 수 있는 방법이다.
이 문제도 그냥 풀게 되면 매우 오래 시간이 걸리기 때문에 원소를 절반으로 나누어 각각의 부분집합을 구한다.
그러면 각각의 부분집합을 구하는데 최악의 경우 2^15 번의 연산을 두 번 하는것으로 2개의 부분집합을 구할 수 있다.
이제 각각의 부분집합을 더한 값이 목표로 하는 C를 넘는지 아닌지 투포인터 알고리즘을 이용해 빠르게 구할 수 있다.
여기서 투포인터 알고리즘을 사용하기 위해 정렬을 해주어야 하므로 O(nlogn)의 시간복잡도로 문제를 해결할 수 있다.
그림으로 보면 아래와 같이 나타난다.
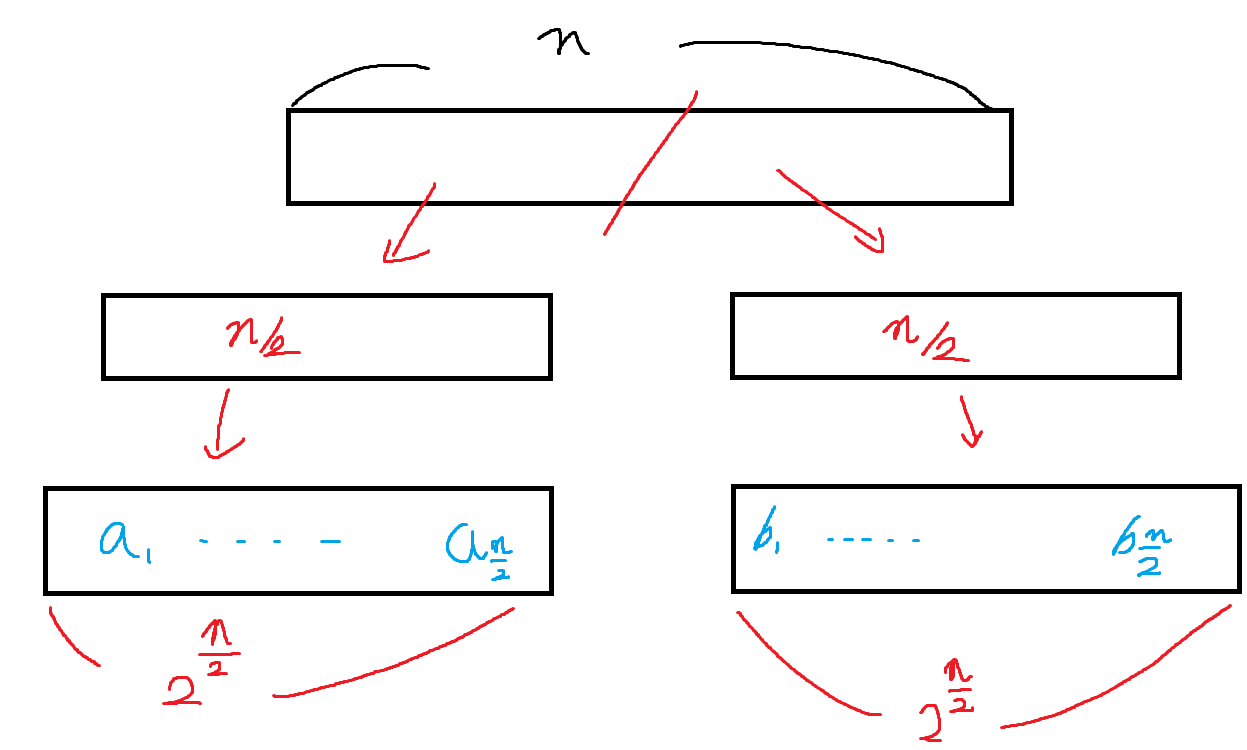
여기서 a와 b는 정렬된 상태이므로 a_i + b_k 의 합이 C를 넘어간다면, b_k-1과 비교한다.
이렇게 a_i와 더한 값이 C보다 같거나 작은 b의 값을 구하면, 조건을 만족하는 b가 몇 개인지 빠르게 구할 수 있다.
(a_(i+1)은 a_i 보다 크기 때문에 a_(i+1)은 이전에 저장된 b_k부터 비교를 하면 된다.)
[아이디어 정리]
- 원소를 절반으로 나누어 두 개의 집합으로 만든다.
- 두 개의 집합에 대하여 각각의 부분 집합들을 만든다.
- 두 개의 부분 집합의 합을 이용해 투포인터 알고리즘으로 조건을 만족하는 부분집합의 개수를 구한다.
Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void MakeSum(vector<long long> &numV, long long sums, int deg, vector<long long> &makeV)
{
if (deg>=numV.size())
{
makeV.push_back(sums);
return;
}
MakeSum(numV, sums, deg+1,makeV);
MakeSum(numV, sums + numV[deg], deg + 1, makeV);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int N,C;
cin >> N>>C;
int middleIdx = N / 2;
vector <long long > nums1(middleIdx);
vector <long long > nums2(N-middleIdx);
int i = 0;
vector<long long> sums1;
vector <long long> sums2;
for (; i<middleIdx; i++)
{
cin >> nums1[i];
}
MakeSum(nums1, 0, 0, sums1);
sort(sums1.begin(), sums1.end());
for (; i<N; i++)
{
cin >> nums2[i-middleIdx];
}
MakeSum(nums2, 0, 0, sums2);
sort(sums2.begin(), sums2.end());
long long ans = 0;
int j = sums2.size()-1;
for (int i=0; i< sums1.size(); i++)
{
while(j>=0&&sums1[i] + sums2[j]>C)
{
j--;
}
ans +=j+1;
}
cout << ans;
return 0;
}
처음에 어떻게 풀어야할지 전혀 감이 오지 않았다.
그러다가 분류에 MITM 알고리즘을 보고나니 어떻게 풀어야 할지 아이디어가 떠올랐다...
분류를 보지 않았다면 푸는데 시간이 얼마나 걸렸을지 모르겠다;;
https://www.acmicpc.net/problem/1450
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] LCS 2 (0) | 2024.05.08 |
|---|---|
| [백준/C++] 가장 긴 증가하는 부분 수열 5 (0) | 2024.05.07 |
| [백준/C++] 소수의 연속합 (0) | 2024.05.04 |
| [백준/C++] 두 용액 (1) | 2024.04.30 |
| [백준/C++] 운동 (0) | 2024.04.23 |