풀이
[문제 풀이]
이 문제는 예전에 풀었던 가장 긴 증가하는 부분수열(LIS) 문제와 비슷하다
단지 차이점이 있다면, 수열의 크기가 크다는 것과 가장 긴 증가하는 부분 수열이 무엇인지 출력을 해야한다는 것이다.
부분 수열의 길이를 구하는 것은 쉽지만, 이 부분수열이 어떻게 이루어져있는지를 구하기 위해서는 기록이 필요하다.
그러면 어떤 방식으로 기록을 해 문제를 해결했는지 아래 그림을 따라 진행하며 알아보자.
먼저 {1,3,5,2,4,5,3} 인 수열이 있다면 아래와 같이 LIS를 찾기 위해 진행 될 것이다.
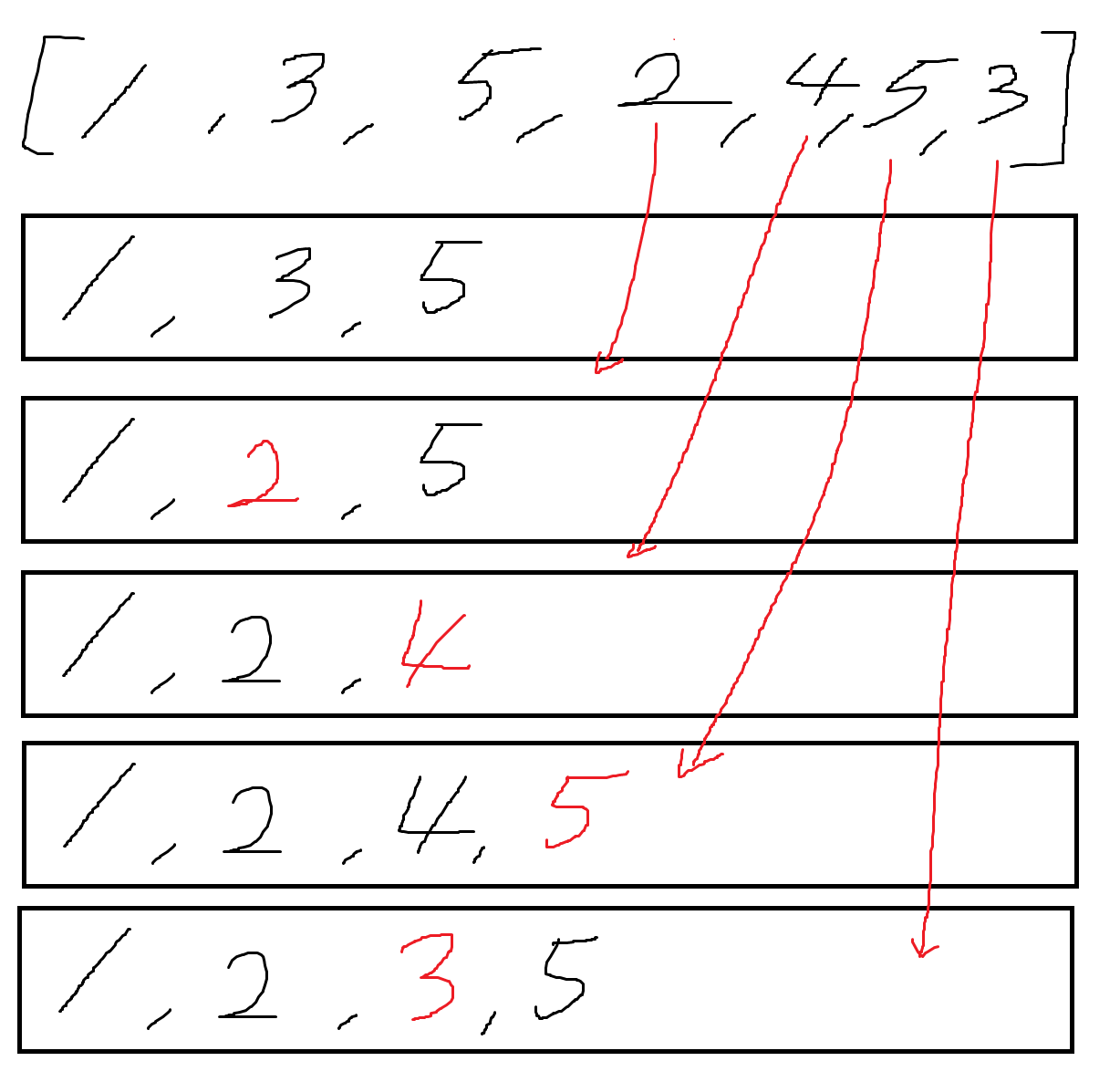
현재 들어온 수가 LIS의 가장 끝에 있는 수보다 작다면, 새롭게 LIS를 갱신한다.
그 이유는 현재 들어온 수 a와 이전에 나왔던 a보다 큰 수 b사이에 있는 수가 뒤에 등장해 새로운 LIS가 생길 수 있기 때문이다.
+ a가 10, b가 100인 경우 뒤에 등장하는 수가 11, 12 등 a와 b사이에 있는 수일 경우 LIS를 바꿔주어야 하기 때문이다.
즉, 새롭게 들어온 수를 포함한 LIS가 있는지 탐색하기 위해 자릿수를 맞춰 LIS를 갱신하는 것이다.
여기서 새로 들어온 수로 LIS를 만들기 위해서는 LIS의 규칙을 유지해야한다.
그러므로 새로 들어온 수는 현재 LIS에서 [i-1]번째 수보다는 크고 기존의 [i]번째 수보다는 작은 조건을 만족하는 위치 i에 저장하면 된다.
여기서 LIS는 정렬되어 있기 때문에 이분탐색을 이용해 빠르게 위치를 찾아 시간을 줄일 수 있다.
이제 LIS를 구하는 방법을 알았으니 LIS를 이루는 수열을 찾기 위해 어떻게 기록을 할지 생각해보자.
방법은 LIS를 만들면서 각 자리의 수가 변할 때 마다 그 위치에 어떤 값이 오는지 기록을 하는 것이다.
즉, 위와 같은 경우에는 아래와 같이 기록을 할 수 있다.
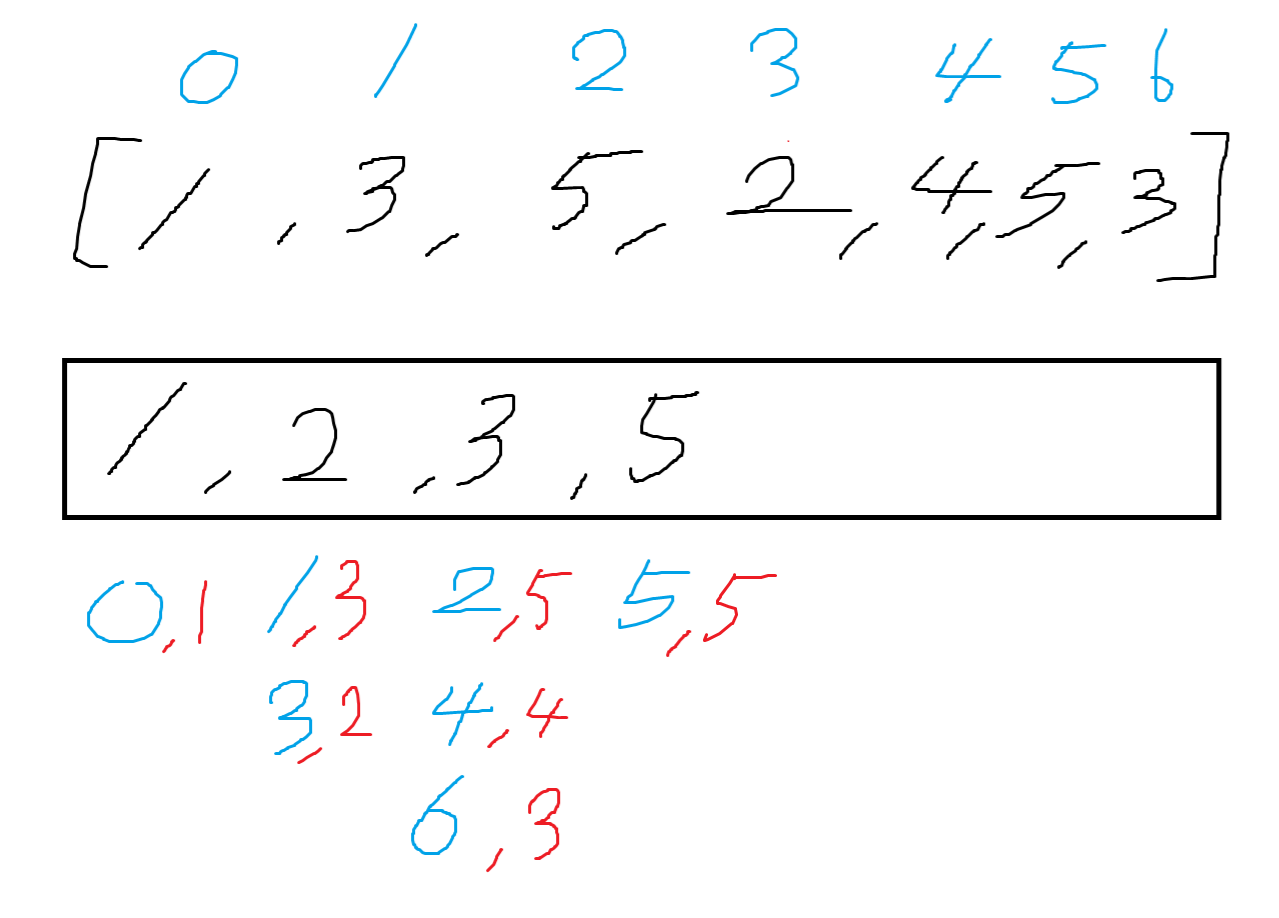
파란색으로 적힌 숫자는 index를 의미하고, 빨간색은 value를 의미한다.
여기서 가장 긴 증가하는 수열을 만들기 위해서는 뒷자리에 있는 수의 index가 앞자리에 있는 index보다 커야 된다.
(왜냐하면 index가 더 큰 수가 앞에 있으면 증가하는 부분 수열이 아니기 때문이다)
즉, 위 그림을 따라 탐색을 시작하면 {1,2,4,5}가 가장 긴 부분 수열 중 하나를 찾을 수 있다.
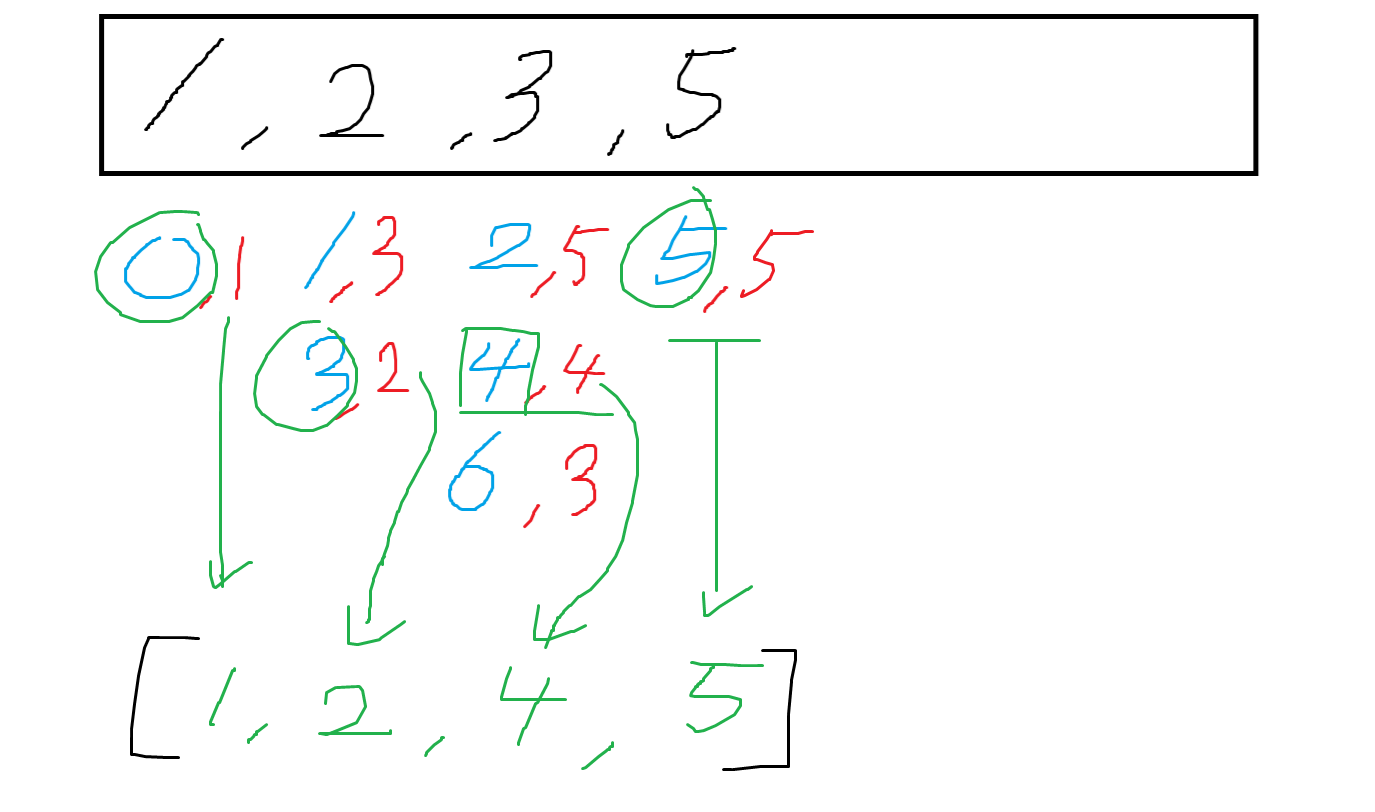
({1,2,3,5} 는 불가능하다. 3은 수열에서 6번째로 등장하는데 5가 5번째로 등장하므로, LIS의 규칙에 따라 {1,2,3,5}의 LIS를 만들 수 없기 때문이다.
+ 값을 비교하지 않고 Index만 비교해도 되는 이유는 LIS를 만드는 방법과 관련이 있다.
LIS를 만들 때, 특정 자리에 새로운 수가 들어오는 경우는 그 자리에 원래 있던 수보다 더 작은 경우다.
그러므로 LIS의 자리수를 s, index를 t, 저장된 value를 v라고 했을 때
$$ s_{i}<s_{j}, \,\,\, t_{i}<t_{j} \,\,를\, 만족하면\, 항상\,\, v_{i}<v{j}\,\, 를\, 만족한다.$$
(그림을 보며 잘 생각해보면 쉽게 이해가 될 것이다.)
[아이디어 정리]
- LIS를 만들때, 새롭게 들어온 수의 위치를 찾기 위해 이분 탐색으로 빠르게 찾는다.
- LIS에 수가 갱신될 때 마다 LIS의 몇 번째 자리에 수열의 몇 번째 index가 들어오는지 저장한다.
- 수열의 탐색을 마치면 LIS의 길이를 출력하고, 뒤에서 부터 LIS를 이루는 수열을 탐색한다.
- 이때, LIS의 규칙에 따라 항상 앞에 오는 수의 index가 뒤에 오는 수의 index보다 작아야 하므로 이 규칙에 맞도록 출력한다.
Code
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int FindIdx(vector<int> &nums, int nowNum)
{
// nowNum의 위치를 찾는 함수, 같으면 큰 것과 마찬가지다 더 작은 index가 어디에 있는지 찾아야 함
// 즉 return할 값이 nowNum보다 작은 수가 있는 index의 위치를 의미한다.
int st = 0, ed = nums.size()-1,mid;
while(st<=ed)
{
mid = (st + ed) / 2;
if (nums[mid]<nowNum)
{
st = mid + 1;
}
else
{
ed = mid - 1;
}
}
return ed;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
vector<int> v(n);
for (int i = 0; i < n; i++) {
cin >> v[i];
}
vector<vector<int>> cV; //등장했던 때
vector<int> nums;
for (int i=0; i<n; i++)
{
if (cV.size() == 0) {
nums.push_back(v[i]);
cV.push_back(vector<int>(1, i));
}
else
{
int jIdx = FindIdx(nums, v[i]);
if (jIdx == nums.size() - 1)
{
nums.push_back(v[i]);
cV.push_back(vector<int>(1, i));
}
else
{
nums[jIdx + 1] = v[i];
cV[jIdx+1].push_back(i);
}
}
}
std::cout << nums.size() << endl;
int nowIdx = cV[cV.size() - 1][cV[cV.size() - 1].size() - 1];
stack<int> st;
st.push(nums[nums.size() - 1]);
for (int i=nums.size()-2; i>=0; i--)
{
int jjj = cV[i].size()-1;
for (int j=jjj; j>=0; j--)
{
if (cV[i][j]<nowIdx)
{
st.push(v[cV[i][j]]);
nowIdx = cV[i][j];
break;
}
}
}
while(!st.empty())
{
cout << st.top() << " ";
st.pop();
}
return 0;
}
LIS를 만드는 방법에 대해 잘 이해하고 있다면, 조금만 생각을 바꿔 쉽게 풀 수 있는 문제였다.
처음에 Index만 비교해도 된다는 사실을 제대로 이해하지 못했는데, 고민해보니 value까지 비교해 LIS를 찾을 필요 없이 그냥 Index만 거꾸로 비교해 출력해도 풀 수 있는 문제였다.
https://www.acmicpc.net/problem/14003
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 경찰차 (0) | 2024.05.09 |
|---|---|
| [백준/C++] LCS 2 (0) | 2024.05.08 |
| [백준/C++] 냅색문제 (1) | 2024.05.05 |
| [백준/C++] 소수의 연속합 (0) | 2024.05.04 |
| [백준/C++] 두 용액 (1) | 2024.04.30 |