문제
https://school.programmers.co.kr/learn/courses/30/lessons/214290
문제 설명
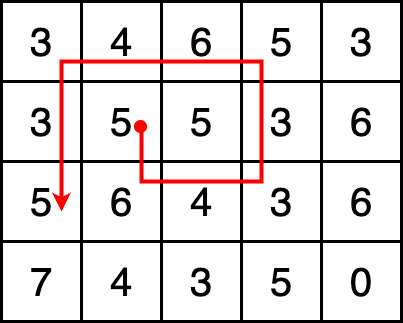
위와 같이 맵이 주어지면 방문할 수 있는 경사로를 [1, -2, -1, 0, 2, 1, -2, -1, 0, 2]와 같은 형태로 주고, 얼마나 경사로를 반복할지 횟수 k를 알려준다.
한번에 이동할 수 있는 경사로는 상하좌우로만 이동할 수 있으며 이전에 방문한 경사로도 방문 할 수 있다.
이때 위 조건을 만족하는 경로의 수를 전부 구해 1000000007로 나눈 나머지를 return하면 된다.
제한사항
- 3 ≤ grid의 길이 = n ≤ 8
- 3 ≤ grid[i]의 길이 = m ≤ 8
- 0 ≤ grid[i][j] ≤ 1,000
- grid[i][j]는 각자의 i+1번째 행, j+1번째 열에 위치한 칸의 높이를 나타냅니다.
- 1 ≤ d의 길이 ≤ 100
- -100 ≤ d의 원소 ≤ 100
- 1 ≤ k ≤ 109
입력, 출력 예시
|
grid
|
d
|
k
|
result
|
|
[[3, 4, 6, 5, 3], [3, 5, 5, 3, 6], [5, 6, 4, 3, 6], [7, 4, 3, 5, 0]]
|
[1, -2, -1, 0, 2]
|
2
|
16
|
|
[[3, 6, 11, 12], [4, 8, 15, 10], [2, 7, 0, 16]]
|
[1, -2, 5]
|
3
|
1
|
|
[[0, 0, 0], [1, 0, 0], [0, 0, 0], [0, 0, 1], [1, 0, 0]]
|
[0, 0, 1, -1, 0, 0, 1, -1]
|
10
|
595737277
|
풀이
문제를 보면 경우의 수가 엄청 많이 나올 수 있음을 알 수 있다. 일단 반복하는 횟수 k가 최대 10^9나 되고 심지어 d의 길이도 100이기 때문이다.
다행인 점은 grid가 8*8이기 때문에 특정 지점A에서 출발해 경사로를 따라 B를 도착하는지 계산하는 것은 BFS로 쉽게 구할 수 있다는 생각이 든다.
문제는 특정 경우인데 만약 [[0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0], ... [0,0,0,0,0,0,0,0]]과 같은 grid에서 경로가 [0,0,0, ... ,0]인 최악의 경우는 계속해서 4 방향씩 방문할 수 있어 BFS로 하더라도 많은 경우의 수가 생길 수 있다.
그렇기 때문에 이를 해결하기 위해 이전에 특정 grid의 지점에 방문했다면, 갈 수 있는 경사로의 개수가 몇개인지 기록된 값을 가져와서 바로 계산하고, 방문한 적이 없다면, 갈 수 있는 경사로의 개수가 몇 개인지 재귀적으로 구하도록 했다.
이 때, n번째에 특정 grid를 방문했을 때 갈 수 있는 경사로의 수와 m번째에 특정 grid를 방문했을 때 경사로의 수가 다를 것이므로, 이를 구분해 몇 번째에 방문했을 때 경사로의 수가 몇 개인지 저장 하도록 Vector를 만들었다.
ex) vector<vector<vector<vector<Seat>>>> rootGoalList
=> [a][b][c] 좌표가 a,b인 grid를 c번째 방문하면 도달할 수 있는 위치 Seat의 정보를 vector로 저장
이렇게 특정 좌표에서 방문할 수 있는 경사로의 좌표와 개수를 전부 구하면 반복하는 횟수 만큼 경사로의 개수를 다시 구해주면된다.
2번 반복할 경우 a좌표에서 도착 할 수 있는 grid의 지점의 경우의 수 * b좌표에서 갈 수 있는 경우의 수 가 a 좌표에서 시작해 경사로의 조건을 만족하는 경우의 수 다.
3번 반복할 경우는 2번 반복했을 때 갈 수 있는 지점의 경우의 수 * 1번 반복했을 때 갈 수 있는 경우의 수로 구할 수 있다.
그러므로 이를 활용하면 최악의 경우 10^9 만큼 반복하는 경우의 수는 이분 탐색으로 빠르게 구할 수 있다.
ex) 1024번 반복 = 512*512 512번 반복 = 256*256 와 같이 나타낼 수 있음
이후 원하는 횟수만큼 반복한 다음 각 위치에서 출발해서 도착할 수 있는 경사로의 경로의 수를 전부 더하면 된다.
[아이디어 정리]
1. BFS로 도착할 수 있는 경사로의 경로의 수를 전부 구한다. (DP를 활용해 횟수 줄이기)
2. 구한 좌표에서 몇번 반복하는지는 이분 탐색을 통해 빠르게 계산한다.
아이디어는 어렵지 않은데 어떻게 횟수를 줄일지와 구한 정보들을 저장할 방법이 고민이 많이 됐다.
Code
#include <string>
#include <vector>
#include <iostream>
#include <bitset>
using namespace std;
struct Seat {
int y;
int x;
long long cnt;
Seat(){
y=0;
x=0;
cnt=0;
}
Seat(int yy,int xx, int cc)
{
y=yy;
x=xx;
cnt=cc;
}
};
vector<vector<int>> realGrid,rootCnt; //rootCnt 는 이 노드를 시작으로 한 노드의 경우의 수를 저장
vector<vector<vector<vector<Seat>>>> rootGoalList;
vector<vector<vector<Seat>>> CanSeatList;
vector<vector<vector<vector<Seat>>>> NCanSeatList; // [a][b][c][<Seat>,<Seat>] a승 y=b, x=c
int gridY,gridX, dSize;
long long constDiv=1000000007;
vector<int> realD;
vector<vector<vector<int>>> visitedV;
int dy[4]={-1,1,0,0};
int dx[4]={0,0,-1,1};
void insertPair(int y, int x, int prevY, int prevX, int nowVisitCnt)
{
Seat cmpS;
bool disCheck;
for (int i=0; i<rootGoalList[y][x][nowVisitCnt].size(); i++)
{
cmpS=rootGoalList[y][x][nowVisitCnt][i];
disCheck=false;
if (nowVisitCnt>0)
{
for (int j=0; j<rootGoalList[prevY][prevX][nowVisitCnt-1].size(); j++)
{
if(cmpS.y==rootGoalList[prevY][prevX][nowVisitCnt-1][j].y&& cmpS.x==rootGoalList[prevY][prevX][nowVisitCnt-1][j].x)
{
rootGoalList[prevY][prevX][nowVisitCnt-1][j].cnt=(rootGoalList[prevY][prevX][nowVisitCnt-1][j].cnt+cmpS.cnt)%constDiv;
disCheck=true;
}
}
// 중복체크 해서 없다면 삽입
if (!disCheck)
{
rootGoalList[prevY][prevX][nowVisitCnt-1].push_back(cmpS);
}
}
}
}
void CalcNode(int y, int x, int nowVisitCnt, int prevY, int prevX)
{
int ny,nx,allCnt;
Seat cmpS;
bool disCheck=false;
if (nowVisitCnt==dSize) //마지막에 도달했으므로 1을 반환한다.
{
Seat goalSeat(y,x,1);
rootGoalList[prevY][prevX][nowVisitCnt-1].push_back(goalSeat);
return;
}
if (visitedV[y][x][nowVisitCnt]==-1)
{
visitedV[y][x][nowVisitCnt]=1;
for (int i=0; i<4; i++)
{
ny=y+dy[i];
nx=x+dx[i];
if (ny>=0&&ny<gridY&&nx>=0&&nx<gridX)
{
if (realGrid[y][x]+realD[nowVisitCnt]==realGrid[ny][nx])
{
CalcNode(ny,nx,nowVisitCnt+1,y,x); //2,0,1,1
}
}
}
// 방문한적이 없다면
insertPair(y,x,prevY,prevX,nowVisitCnt);
return;
}
else
{
insertPair(y,x,prevY,prevX,nowVisitCnt);
return;
}
}
void SeatInitaial()
{
vector<vector<vector<Seat>>> NewSeatList;
vector<vector<Seat>> SeatVector(gridX,vector<Seat>(0));
for (int i=0; i<gridY; i++)
{
NewSeatList.push_back(SeatVector);
}
CanSeatList=NewSeatList;
}
void SeatSave(vector<vector<vector<Seat>>> NewNSeat) //int n == n승
{
NCanSeatList.push_back(NewNSeat);
return;
}
vector<vector<vector<Seat>>> AmultiB(vector<vector<vector<Seat>>> aSeat,vector<vector<vector<Seat>>> bSeat) // 계산
{
vector<vector<vector<vector<bool>>>> disCheckV(gridY, vector<vector<vector<bool>>>(gridX,vector<vector<bool>>(gridY,vector<bool>(1,false))));
vector<vector<vector<Seat>>> returnSeat;
vector<vector<Seat>> SeatVector(gridX,vector<Seat>(0));
for (int i=0; i<gridY; i++)
{
returnSeat.push_back(SeatVector);
}
for (int i=0; i<gridY; i++)
{
for (int j=0; j<gridX; j++)
{
for (int k=0; k<aSeat[i][j].size(); k++)
{
Seat aaS=aSeat[i][j][k]; //
for (int bk=0; bk<bSeat[aaS.y][aaS.x].size(); bk++)
{
Seat bbS=bSeat[aaS.y][aaS.x][bk]; //bbs.y는 종점 i,j에서 어디에 도달할 수 있는지를 i,j에 저장하는 것
bbS.cnt=(bbS.cnt*aaS.cnt)%constDiv;
bool disC=false;
for (int hcnt=0; hcnt<returnSeat[i][j].size(); hcnt++)
{
if (returnSeat[i][j][hcnt].y==bbS.y&&returnSeat[i][j][hcnt].x==bbS.x)
{
returnSeat[i][j][hcnt].cnt=(bbS.cnt+returnSeat[i][j][hcnt].cnt)%constDiv;
disC=true;
break;
}
}
if (!disC)
{
returnSeat[i][j].push_back(bbS);
}
}
}
}
}
return returnSeat;
}
void AnsCalc(long long k) //k를 2진수로 변환해서 가장 상위에 있는 것 계산 30번 정도면 될듯
{
for(int i=0; i<39; i++)
{
NCanSeatList.push_back(AmultiB(NCanSeatList[i],NCanSeatList[i]));
}
bool flag=false;
string flagString="";
string flagString2="";
vector<vector<vector<Seat>>> realSeat;
bitset<sizeof(int) * 8> binaryK(k);
flagString2= binaryK.to_string();
for (int i=0; i<flagString2.length();i++)
{
flagString=flagString2[i]+flagString;
}
작성한 코드를 보면 엄청나게 길이가 긴 것을 알 수 있다...
처음에 어떻게 a에서 b로 가는 것과 a에서 c로 가는 경우의 수를 전부 더해버리는 바람에 한번 코드가 꼬였고, 이를 재사용하려다 보니 코드가 길어지고... 심지어 갈 수 있는 위치를 <pair>로 저장해 둬서 코드를 많이 수정했다.
심지어 vector를 초기화하는 것도 헷갈리고 종이가 없다보니 구조체를 만들기 전에는 vector<vector<vector<vector<vector<int>>>>>> 로 BFS를 계산할 뻔 했다;; 지금도 한 번 줄어든 상태;
나중에는 분명 계산한 대로 구해지고 답도 맞는데 특정 TC에서 자꾸 틀리는 상황도 발생했다.
아무리 코드를 보고 고쳐봐도 답이 맞는 것 같은데 틀렸다고 뜨길래 왜 그런지 고민하는데, 연산 시간이 좀 긴 경우에만 발생한 것을 보고, Type관련된 오류일 것 같다고 생각이 들었다.
그래서 long long으로 바꿔줬는데 그래도 해결이 안됐다.
알고보니 1번 방문하는 경우를 BFS로 구할 때 더하는 부분에서 1000000007로 나머지를 안나눠 줘서 생긴 오류였다.
자려고 누워있다가 반복하는 횟수가 1인 경우에 4^1000의 경우의 수도 있겠다는 생각이 들어서 다음날 일어나자마자 고치니까 바로 풀렸다.
C++ 타입이랑 vector등 STL사용이 아직도 익숙하지 않은 부분이 있다... 파이썬 그리워ㅠㅠㅠㅠㅠ
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/Python] 정수 삼각형 (0) | 2024.01.05 |
|---|---|
| [프로그래머스/C++] 풍선 터트리기 (1) | 2024.01.05 |
| [프로그래머스/C++] 숫자 게임 (1) | 2024.01.04 |
| [프로그래머스/C++] 야근 지수 (1) | 2024.01.03 |
| [프로그래머스/Python] 하노이의 탑 (1) | 2024.01.02 |