문제
https://school.programmers.co.kr/learn/courses/30/lessons/12946
하노이 탑은 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있다. 게임의 목적은 다음 두 가지 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것이다.
- 한 번에 하나의 원판만 옮길 수 있습니다.
- 큰 원판이 작은 원판 위에 있어서는 안됩니다.
하노이 탑의 세 개의 기둥을 왼쪽 부터 1번, 2번, 3번이라고 하면, 1번에는 n개의 원판이 있고 이 n개의 원판을 3번 원판으로 최소 횟수로 옮기려고 한다.
이 때, 1번 기둥에 있는 원판의 개수 n이 매개변수로 주어지면 n개의 원판을 3번 원판으로 최소로 옮기는 방법을 return하는 solution를 하면 된다.
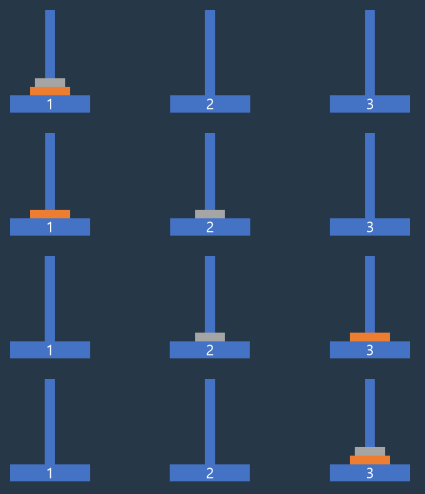
풀이
하노이 탑은 쉽게 생각하면 된다. 1개의 블록만 있으면 1에서 3으로 옮긴다. 2개의 블록이 있을 경우 첫번째 블록을 1에서 2로 옮기고 두번째 블록을 1에서 3으로 옮긴 뒤 첫번째 블록을 다시 2에서 3으로 옮긴다.
블록이 3개일 경우 2개의 블록을 1에서 2로 옮기고 3번째 블록을 1에서 3으로 옮긴 뒤, 다시 2번에 있는 2개의 블록을 3으로 옮기면 된다. 이를 표현하면 다음과 같이 표현할 수 있다.
[n개의 블록을 1에서 3으로 옮기는 방법]
1. [n-1개의 블록을 1에서 2로 옮긴다]
2. [n번째 블록을 1에서 3으로 옮기기]
3. [n-1개의 블록을 2에서 3으로 옮기기]
여기서 n-1개의 블록을 원하는 위치로 옮기는 방법도 똑같다.
마찬가지로 n-2개의 블록을 1에서 3으로 옮기고, n-1번째 블록을 1에서 2로 옮긴 뒤, n-2개의 블록을 3에서 2로 옮기면 된다.
즉, [n개를 1에서 3으로] = [n-1개를 1에서 2로]+[n을 1에서 3으로]+[n-1개를 2에서 3으로]
재귀적으로 만들면 된다.
Code
def hanoi(st,mid,ed, num):
if num==1:
return [[st,ed]]
else :
# lst=[]
# st_to_mid=hanoi(st,ed,mid,num-1)
# mid_to_ed=hanoi(mid,st,ed,num-1)
# for i in st_to_mid:
# lst.append(i)
# lst.append([st,ed])
# for i in mid_to_ed:
# lst.append(i)
# return lst
return hanoi(st,ed,mid,num-1)+[[st,ed]]+hanoi(mid,st,ed,num-1)
def solution(n):
# n개를 옮기기 => n-1개를 2번으로 옮기고 n번째를 3으로 옮기고 n-1개를 2에서 3으로 옮기기
answer = hanoi(1,2,3,n)
return answer
오랜만에 문제 푸니까 문제보다 2차원 배열로 형식 맞추는게 더 힘들었네...
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/Python] 정수 삼각형 (0) | 2024.01.05 |
|---|---|
| [프로그래머스/C++] 풍선 터트리기 (1) | 2024.01.05 |
| [프로그래머스/C++] 경사로의 개수 (2023 현대모비스 알고리즘 경진대회 예선) (0) | 2024.01.05 |
| [프로그래머스/C++] 숫자 게임 (1) | 2024.01.04 |
| [프로그래머스/C++] 야근 지수 (1) | 2024.01.03 |

