[SWEA/C++] DAG 동전 게임

문제

문제 설명

 

 

풀이

 

[문제 풀이]

 

이 문제는 설명을 잘 이해해야 쉽게 풀 수 있는 문제다.

 

먼저 조건을 보면 사이클이 있으며 위상 정렬이 되어있다.

이를 이용하면 DFS로 1번 노드부터 시작해 N번노드와 N-1번 노드에 도착하는 경우에 돈을 얼마 미만 갖고 있어야 하는지 파악 할 수 있다.

 

먼저 그림을 통해 예를 들어 보자.

 

위 그림과 같은 경우에는 N-1과 N으로 바로 가는 방법이 있다.

그러므로 다현의 돈의 비율이 나연의 비율과 같은 1:1 미만이면 무조건 나연이 승리한다는 사실을 알 수 있다.

 

이번에는 조금 다른 경우를 그려보자

 

 

위 그림을 보면 N-1과 직접 연결된 경로가 있으면 가진 돈을 전부 제시해 N-1로 가도록 유도할 수 있다.

그러므로 다현은 나연이 가진 모든 돈보다 조금 많도록 제시해 오른쪽으로 가도록 경로를 바꾸는게 최선이다.

이때, 오른쪽으로 갔을 때도 나연이 이기려면 이동 후에 비율이 1:1을 유지하면 된다는 것을 알 수 있다.

 

그러므로 위 그림을 통해 바로 N이나, N-1으로 가는 경로가 있다면, 상대방의 돈 만큼의 액수를 더해주면 된다는 사실을 알 수 있다.

 

만약 N-1이 아니라 N이라면 다현의 돈이 2배 더 많게 됨 

 

이제 이를 이용하면 직접 연결된 경우를 제외하면 일반식으로 모든 경로에 대해 얼마만큼의 돈을 갖고 있어야 하는지 판단할 수 있게 된다.

 

 

그림에서 각 경로 별 돈의 비율이 위와 같이 나타났다고 생각해보자

 

그러면 다현 입장에서는 나연이 돈을 많이 가져야하는 경로로 이동하는게 유리하고, 나연 입장에서는 다현이 돈을 많이 가져야하는 경로로 이동하는게 유리하다.

 

그러므로 둘은 a만큼의 돈을 더 지불하더라도 상대방과 돈의 비율이 승리하도록 제시할 수 있다.

 

이를 이용해 부등식으로 표현하면 위와 같이 나타낼 수 있다.

이후 지불 가능한 돈인 a를 연립해 제거하면 최대 x를 구할 수 있다.

 

왜 연립해 제거 해야하는지는 가로축이 a, 세로축이 x인 그림을 그려보면 쉽게 이해할 수 있다.

 

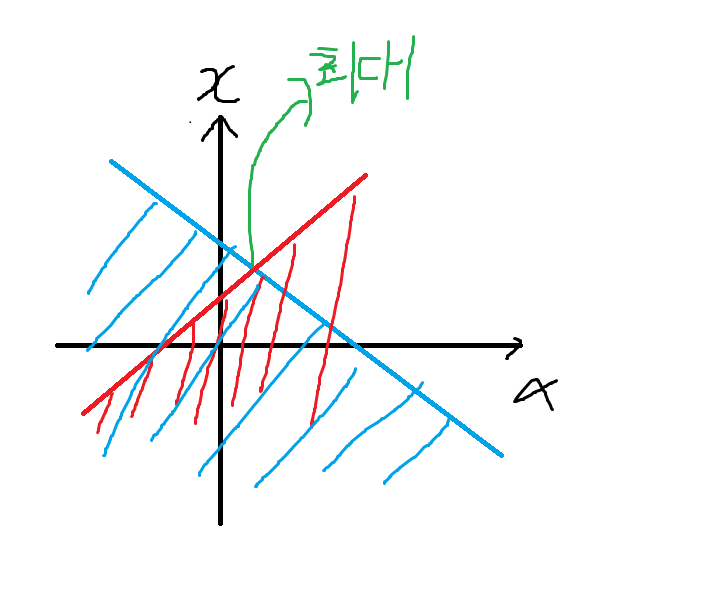
이제 일반식도 구했으므로 나연이 유리한 경우의 돈의 비율을 1:maxV, 다현이 유리한 경우의 돈의 비율을 1:minV 로 표현하면 아래와 같은 답을 구할 수 있다.

 

1 : maxV(1+minV)/(1+maxV)

 

이를 이용하면 최종적으로 구해진 비율에 10000원을 곱해 얼마의 돈 미만이면 나연이 무조건 이기는지 구할 수 있다.

 

 

 

[아이디어 정리]

1. DFS로 각 경로별로 나연이 무조건 이기기 위해 다현이 얼마의 돈을 가지고 있어야하는지 비율을 계산한다.
2. 비율을 계산할 때, 직접 N, N-1과 연결된 경로가 있는 경우를 따로 계산한다.
3. 나연이 가장 유리한 경로와 다현이 가장 유리한 경로가 N과 N-1과 직접 연결되어 있지 않다면 비율을 이용해 계산한다.
4. 비율을 이용해 계산하는 방법은 나연이 유리한 경우를 maxV, 다현이 유리한 경우가 minV 일 때, maxV(1+minV)/(1+maxV) 이다.

 

 

Code

 

 

#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
using namespace std;

const int INF = 200;
long double calc(int n, vector<vector<int>> &graph, vector<long double> &VM, int N)
{
	if (n==N)
	{
		return 0;
	}
	else if (n == N - 1) {
		return INF;
	}
	else if (VM[n]==-1)
	{
		// min = 나연이 이기는 가장 작은 비율, 1:x
		// max = 나연이 이기는 가장 큰 비율
		// 비율이 크면 더 많은 돈을 쓰게 만들 수 있음
		long double minV, maxV, tmp;
		minV = INF, maxV = 0;
		bool N0 = false, N1 = false; // N과 N-1에 바로 가는 그래프가 있는 지?
		for (int i=0; i<graph[n].size(); i++)
		{
			tmp = calc(graph[n][i], graph, VM, N);
			minV = min(minV, tmp);
			maxV = max(maxV, tmp);
		}
		if (minV==maxV)
		{
			VM[n] = minV;
			return VM[n];
		}
		else if (minV==0 &&maxV==INF)
		{
			VM[n] = 1;
			return VM[n];
		}
		else if (minV==0)
		{
			VM[n] = maxV / (1 + maxV);
			return VM[n];
		}
		else if (maxV==INF)
		{
			VM[n] = 1 + minV;
			return VM[n];
		}
		else
		{
			VM[n] = maxV*(1 + minV) / (1 + maxV);
			return VM[n];
		}

	}
	else {
		return VM[n];
	}
}

int main()
{
	/*ios::sync_with_stdio(false);
	cin.tie(0);*/
	cout << fixed;
	cout.precision(9);
	int tc;
	cin >> tc;	
	for (int T=0; T<tc; T++)
	{
		int N, M; 
		cin >> N >> M;
		vector<vector<int>> graph(N + 1);
		int a, b;
		priority_queue<int> q;
		vector<long double> VM(N + 1, -1);
		for (int i=0; i<M; i++)
		{
			cin >> a >> b;
			graph[a].push_back(b);
		}
		long double ans = calc(1, graph, VM, N);
		if (ans==INF)
		{
			cout << -1 << endl;
		}
		else
		{
			cout << 10000 * ans << endl;
		}

	}
}

---

 

처음에 문제를 풀 때 문제가 잘 이해가 안 됐던 문제다.

 

하지만 잘 생각해보면 다현이 얼마 미만의 돈을 가지면 되는지 구하는 문제이므로 10000, 10000을 가지고 있을 경우 무조건 나연이 더 많은 돈을 제시한다고 생각하면 되는 문제였다...

 

일반식 구할 때도 헷갈릴 뻔 했는데, 지금 생각해보면 왜 헷갈렸는지 잘 모르겠다;;

 

 

https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AZIitY1a5P4DFAXd&categoryId=AZIitY1a5P4DFAXd&categoryType=CODE&problemTitle=&orderBy=FIRST_REG_DATETIME&selectCodeLang=ALL&select-1=&pageSize=10&pageIndex=1