풀이
[풀이]
서로 다른 동전은 서로 배수관계를 갖고 있다.
만약 V_i와 V_(i+1)이 2배 차이라면 V_i원의 동전의 2배가 되는 돈을 요청 하게 되면 은행은 V_(i+1)원 동전 하나를 주게 된다.
그러므로 V_i원의 동전의 색을 확인하려면 요구하는 돈 X는 V_i <= X < V_(i+1) 여야 한다. 즉, V_(i+1)이 V_i의 n 배수라면 V_i 동전을 최대 n-1개 받을 수 있다는 뜻이다. (V_i 동전을 n개 받는 경우의 수는 없다.)
가장 큰 금액의 동전의 경우 몇개를 요청하던 가장 큰 금액의 동전으로 주기 때문에 구분 할 수 있다.
이를 아래와 같이 나타낼 수 있다.
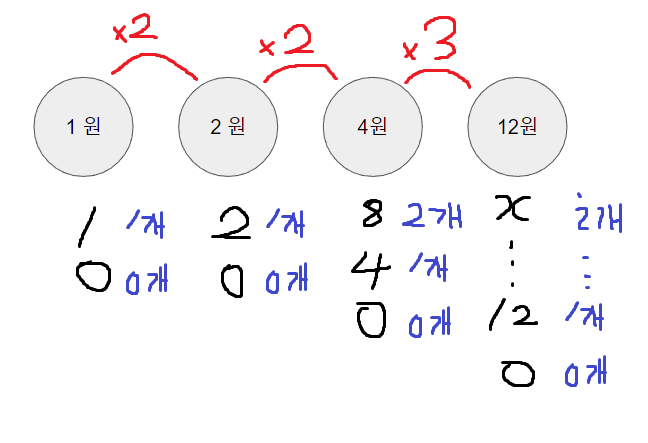
위의 그림에서 알 수 있는 점은 V_i와 V_(i+1)이 n배수일 경우 V_i 동전은 한 회차에 0 ~ n-1사이의 수 중 하나를선택해 받을 수 있다. (4원을 2개 받고 2원을 1개 1원을 1개 받으려면 11원을 요청 하면 된다.)
즉, 우리는 한 회차에 n배수의 동전을 받는 경우는 n가지 이며, 2회차에는 n^2으로 받고, 3회차에는 n^3의 경우의 수로 받을 수 있다.
아래 표의 m회차 아래에 적힌 수는 m회차에 받은 동전의 개수이다.
|
2배수
|
1회차
|
2회차
|
3회차
|
|
1
|
0
|
0
|
1
|
|
2
|
0
|
1
|
0
|
|
4
|
0
|
1
|
1
|
|
8
|
1
|
0
|
0
|
|
16
|
1
|
0
|
1
|
|
32
|
1
|
1
|
0
|
|
64
|
1
|
1
|
1
|
|
128
|
|
|
|
이를 표로 표현하면 다음과 같다 각 회차마다 V_i원의 동전의 개수를 다음과 같이 요청해 전부 구분 할 수 있다.
(1회차 ~ 3회차를 0, 0, 0으로 받을 경우 구분할 수 없다. 동전을 받지 않았으므로 색을 구분할 수 없기 때문에)
이를 활용해 n배수의 관계를 세고 n배수의 관계가 x개 있다면 x개의 관계를 갖는 동전을 구분하기 위해서는 m회차에서 $$x<(n^m)-1$$
의 관계를 만족하는 가장 작은 m의 수를 구해야 한다.
이때 배수 관계가 2, 3 등 여러개의 배수 관계를 가질 때는 순차적으로 구했다.
예를 들어 3배수의 관계를 갖는 동전의 경우 회차마다 받을 수 있는 동전의 개수는 0,1,2 이지만 2배수 관계를 갖는 동전이 0, 1의 경우를 선택하므로 2배수 동전을 0, 1개 받는 경우와 3배수 동전을 0, 1개 받는 경우를 구분 할 수 없다.
그래서 2배수 관계에서 최소 m회차를 구한 다음 3배수 관계에서 m회차를 구할 때는 (2배수 관계의 수+3배수 관계의 수)가 $$(3^m)-1$$
보다 작거나 같은 최소 m을 구했다.
Code
def fx(dic): # n=배수
a=0
ans=[] # 각 배수마다 몇 회차가 필요한지 저장할 리스트
for i in dic.keys(): # dic의 key는 i배수 관계 value는 n배수 관계가 몇 개 인지
num=1 # num==회차
k=i-1 # 1회차에 i배수에서 i-1개의 관계를 구분 할 수 있음
a+=dic[i] # 이전 배수의 개수에 현재 i배수 관계의 수를 더한다.
while a>k:
num+=1
k=(i**num)-1 # num회차에 구분할 수 있는 경우의 수는 최대 i^num-1이므로
ans.append(num) # ans에 저장
return max(ans) # 저장한 최소 회차 중 가장 큰 회차를 return
for tc in range(1, 1 + int(input())):
N = int(input()) # 동전 개수
lst = list(map(int, input().split()))
ans = []
if len(lst) <= 2: # 동전의 개수가 2보다 작거나 같으면 1회차에 구분 가능하다
print(f'#{tc} {1}')
else:
dic=dict()
for i in range(N - 1):
ans.append(lst[i + 1]//lst[i])
ans_set =list(set(ans))
ans_set.sort()
for i in ans_set:
dic[i]=ans.count(i) # dic에 n배수 관계가 몇 개인지 count
print(f'#{tc} {fx(dic)}')
이 문제를 다르게 생각하면 n배수=n진법과 같으므로(2진법=0,1로 수를 표현 3진법= 0,1,2로 수를 표현 ... 이때 2진법으로 표현한 11과 3진법으로 표현한 11을 구분 할 수 없다.) n진법의 자릿수로 표현할 수 있는 수의 개수를 묻는 문제와 같은 맥락이다.
맨 처음에 낸 아이디어도 비슷했는데, 경우의 수를 잘못 계산하고 코딩도 실수해서 풀지 못했다.
이후 아이디어를 설명하다가 잘못된 부분이 떠올라 경우의 수 부분을 수정했고 정답을 맞췄다
아이디어는 빨리 냈는데 문제를 푸는데 오래 걸려서 당황했던 문제다...
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
'Algorithm > SWEA' 카테고리의 다른 글
| [SWEA/C++] 서로소 그리드 (No. 20731) (0) | 2024.06.19 |
|---|---|
| [SWEA/Python] 17643번 - 로봇 (0) | 2024.01.05 |
| [SWEA/C++] 2112. [모의 SW 역량테스트] 보호 필름Box에 담기 문제 풀기 (0) | 2024.01.05 |
| [SWEA/Python] 5250 - 최소비용 (0) | 2024.01.05 |
| [SWEA/Python] 5249 - 최소 신장 트리 (0) | 2024.01.05 |