풀이
[문제 풀이]
이 문제는 LCS를 찾는 문제인데, 특이한 조건이 있다.
바로 수열의 크기 N이 주어지면 1~N의 숫자를 가진 순서가 다른 수열이 2개 주어진다는 것이다.
만약 이 조건을 대충 넘기고 그냥 풀게 되면 조건으로 주어지는 N이 10만이므로 일반적인 LCS로 문제를 풀게되면 O(N^2)으로 시간초과가 나게 될 것이다.
이제 어떻게 하면 O(N^2)보다 빠르게 문제를 풀 수 있을지 생각해보자.
잘 생각해보면 1~N의 숫자가 2개의 수열에 한 번만 등장하기 때문에 하나의 수열의 i번째 index가 다른 수열의 몇 번째 자리에 있는지 바꾼다면 LCS문제를 LIS문제로 풀 수 있게 된다.
일단 LCS의 풀이에 대해 생각해보자.
수열 A, B가 있을 때, 공통 부분 수열에 어떤 숫자 i가 포함된다고 가정하면, 숫자 i 다음에 올 수 있는 수는 어떤 수일까?
숫자의 조건을 생각해보면 A 수열에서 i가 나온 이후에 나온 수 이면서 B수열에서 i가 나온 뒤에 있는 수여야 한다.
즉, 공통 수열의 i라는 숫자 뒤에 올 수 있는 수는 A와 B 수열에서도 숫자 i 뒤에 있어야 한다는 뜻이 된다.
이를 이용하면 A 수열을 기준으로 숫자들은 이미 index가 정렬됐으므로 B 수열의 index가 A수열에서 몇 번째에 등장하는지 기록을 하면 그 기록을 이용해 LIS로 문제를 풀 수 있다. (LIS로 풀면 시간복잡도 O(nlogn)으로 풀 수 있다.)
이제 아래 그림을 보며 더 쉽게 이해해 보자.
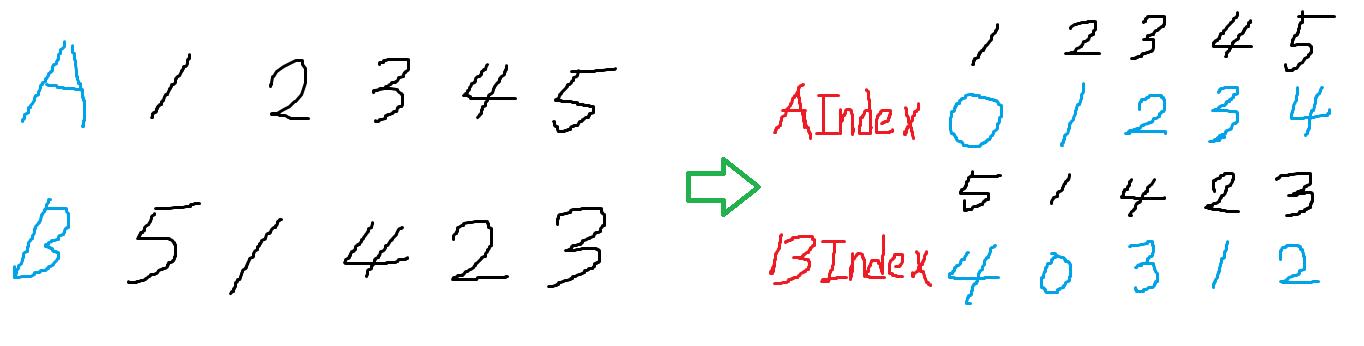
A 수열은 [1, 2, 3, 4, 5] 순서로 수열이 이루어져있고, B수열은 [5, 1, 4, 2, 3]이다.
이제 B 수열의 숫자들을 A 수열의 index로 변경해보자.
그러면 5는 A수열의 4번째 자리, 1은 A수열의 0번째 자리, 4는 A수열의 3번째 자리, 2는 A수열의 1번째 자리, 3은 A수열의 2번째 자리이다.
이렇게 변경해주면 [4, 0, 3, 1, 2]가 된다.
여기서 [4, 0, 3, 1, 2]의 의미를 다시 짚고 넘어가면 B수열의 0번째 숫자는 A수열에 4번째 자리에 있고, 1번째 숫자는 0번째 자리에 있다는 뜻이다.
B수열에 A수열의 Index를 매칭했기 때문에, A수열은 이미 부분수열의 순서대로 정렬된 것이나 마찬가지다.
그러므로 B수열에 저장된 숫자를 이용해 LIS를 구하면 공통 수열이 되는 것이다.
또 다른 예를 보며 생각을 정리해보자.

이전의 풀이와 전혀 다르지 않다.
A수열이 [2, 1, 4, 3, 5] 순서대로 되어있으므로 이 index를 B수열에 매치하면 A수열에서 [0, 1, 2 ,3, 4] 순서대로 나오는 수는 B 수열에 [4, 2, 0, 1, 3]순서로 나온다.
즉, A수열은 이미 순서대로 정렬되어 있으므로, B수열에 LIS만 구하면 LIS의 길이가 최장 공통 수열의 길이가 된다.
이를 이용하면 B에서 계산한 LIS는 [0, 1, 3] 이며, 이 0, 1, 3은 A배열의 Index를 의미한다.
다시 index를 수로 변환하면 [2, 1, 3]이 되고 이 [2, 1, 3]의 수가 실제로 A와 B의 LCS라는 것을 알 수 있다.
LIS 문제
[아이디어 정리]
- 모든 수가 한번 씩 나오기 때문에 중복되는 수가 나오지 않는다.
- 그러므로 하나의 수열 A를 기준으로 숫자가 나온 순서(Index)를 파악하고, B수열에 매칭한다.
- 그러면 A수열은 이미 [0, 1, 2 ..] 순서로 숫자가 정렬된 상태이고, B수열은 A번째 수열과 index가 매칭된 상태가 된다.
- A의 Index를 이용하므로 B 수열에 매칭된 수를 이용해 계산한 LIS는 A에 무조건 존재할 수 있다.
- 그러므로 B 수열의 LIS를 구하면 A와 B 수열의 LCS가 된다.
Code
#include <string>
#include <vector>
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
void FindLIS(int num, vector<int>&LIS)
{
int st = 0, ed = LIS.size()-1, mid;
while (st <= ed) {
mid = (st+ed) / 2;
if (LIS[mid] < num)
{
st = mid + 1;
}
else {
ed = mid - 1;
}
}
if (st >= LIS.size()) {
LIS.push_back(num);
}
else {
LIS[st] = num;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int N;
cin >> N;
vector<int> nToIdx(N+1);
int num;
for (int i = 0; i < N; i++)
{
cin >> num;
nToIdx[num] = i;
}
vector<int> LIS;
cin>>num;
LIS.push_back(nToIdx[num]);
for (int i = 1; i < N; i++)
{
cin >> num;
FindLIS(nToIdx[num], LIS);
}
cout << LIS.size();
return 0;
}
LIS와 LCS에 대해 잘 이해하고 있으면 쉽게 풀 수 있는 문제였다.
이해가 잘 안된다면, LCS의 조건과 문제의 조건을 읽어보고 예시를 따라 수를 써보면 더 이해가 잘 될 것 같다.
오랜만에 재미있는 문제였다.
https://www.acmicpc.net/problem/13711
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 사이클 게임 (No. 20040) (0) | 2024.05.28 |
|---|---|
| [백준/C++] 친구 네트워크 (No. 4195) (0) | 2024.05.26 |
| [백준/C++] 하이퍼 토마토 (0) | 2024.05.26 |
| [백준/C++] 여행 가자 (No. 1976) (0) | 2024.05.25 |
| [백준/C++] 집합의 표현 (No. 1717) (0) | 2024.05.24 |