풀이
[문제 풀이]
이 문제를 처음 봤을때 고민을 많이 했다.
좌표의 범위가 매우 크기 때문에 모든 좌표를 직접 검사하는 것은 불가능하다.
그래서 처음 했던 생각은 시작 좌표에서 거꾸로 쿼리를 진행하면, 더 빠르게 체크를 할 수 있겠다고 생각이 들었다.
x좌표와 y좌표는 서로 영향을 미치지 않으므로 1차원 좌표를 그려 풀이를 생각해보자
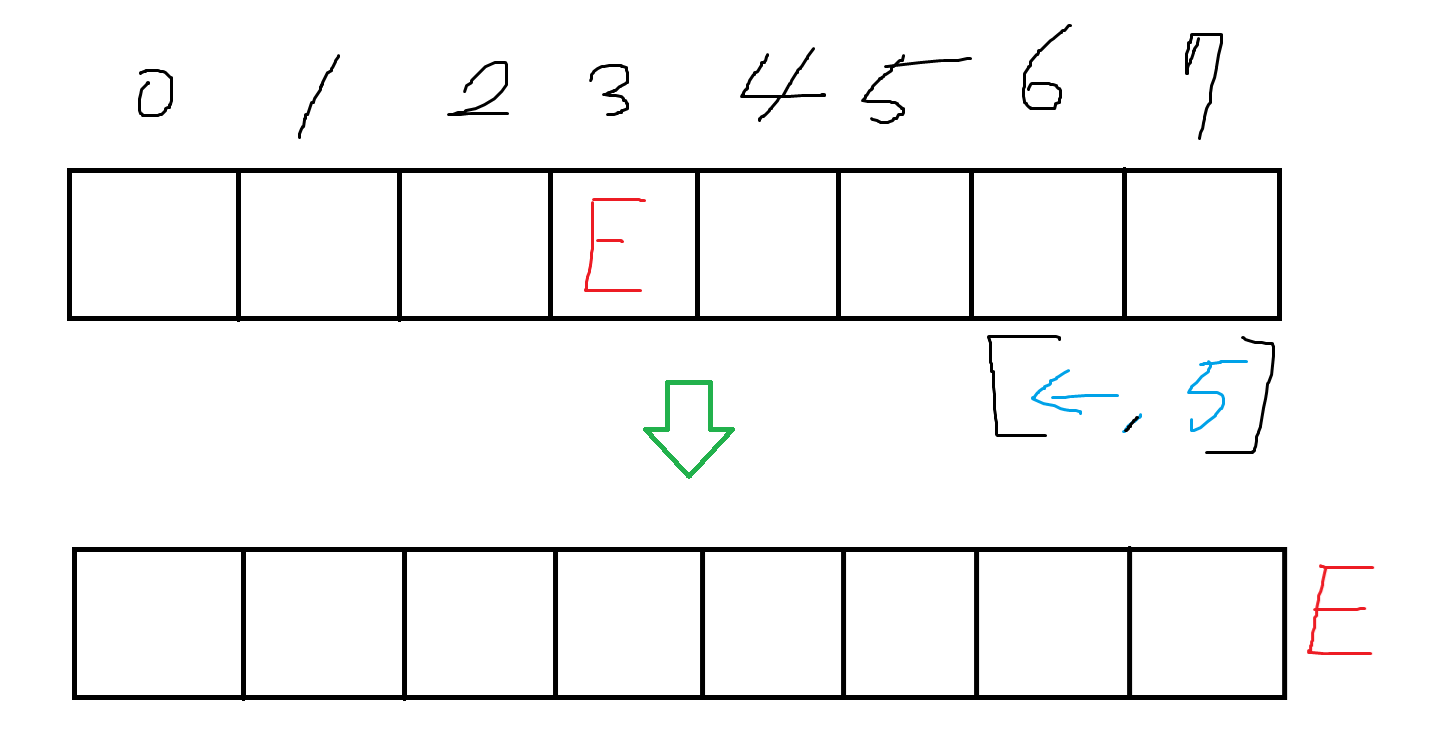
위 그림과 같이 쿼리를 거꾸로 진행하는데 왼쪽으로 5번 이동하라는 쿼리가 나오는 경우를 생각해보자.
이때 도착점이 3이 되려면 이전에 E의 위치는 8이여야 하는데, 실제 좌표는 7까지이므로 불가능한 경우다.
그렇다면 항상 좌표의 범위를 벗어나면 불가능한 경우일까?
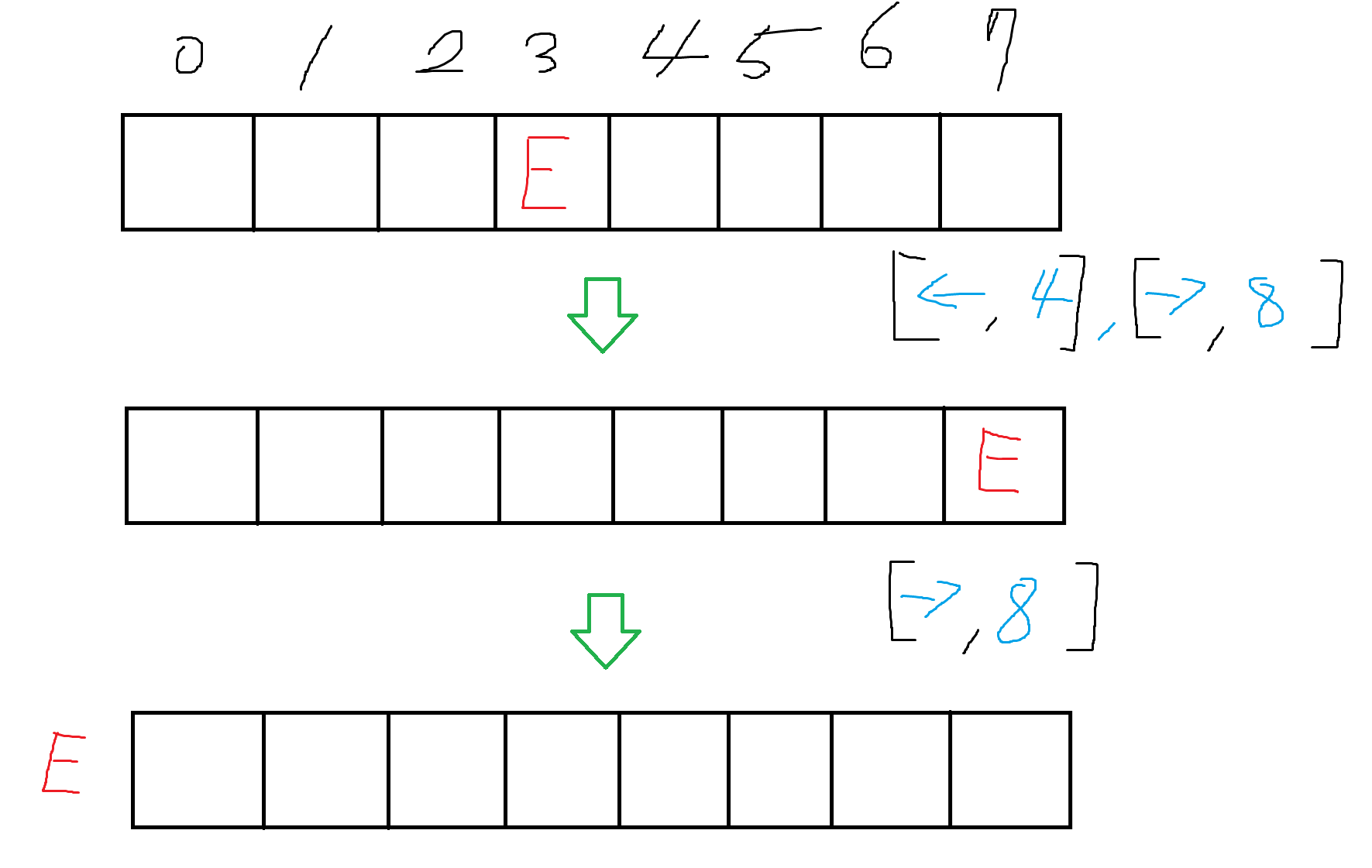
위 경우에서는 E가 -1로 범위 바깥에 위치하게 되지만, 3좌표에 도달할 수 있는 경우다.
이와 같은 차이가 생기는 이유는 두번째 경우는 방향이 바뀌기 전에 반대쪽 벽에 닿고 범위를 벗어났기 때문이다. (중요)
거꾸로 진행하다 보면 헷갈릴 수 있으니 쿼리의 순서를 따라가는 예를 들어보겠다.
좀 더 간단하게 그린 그림을 보면
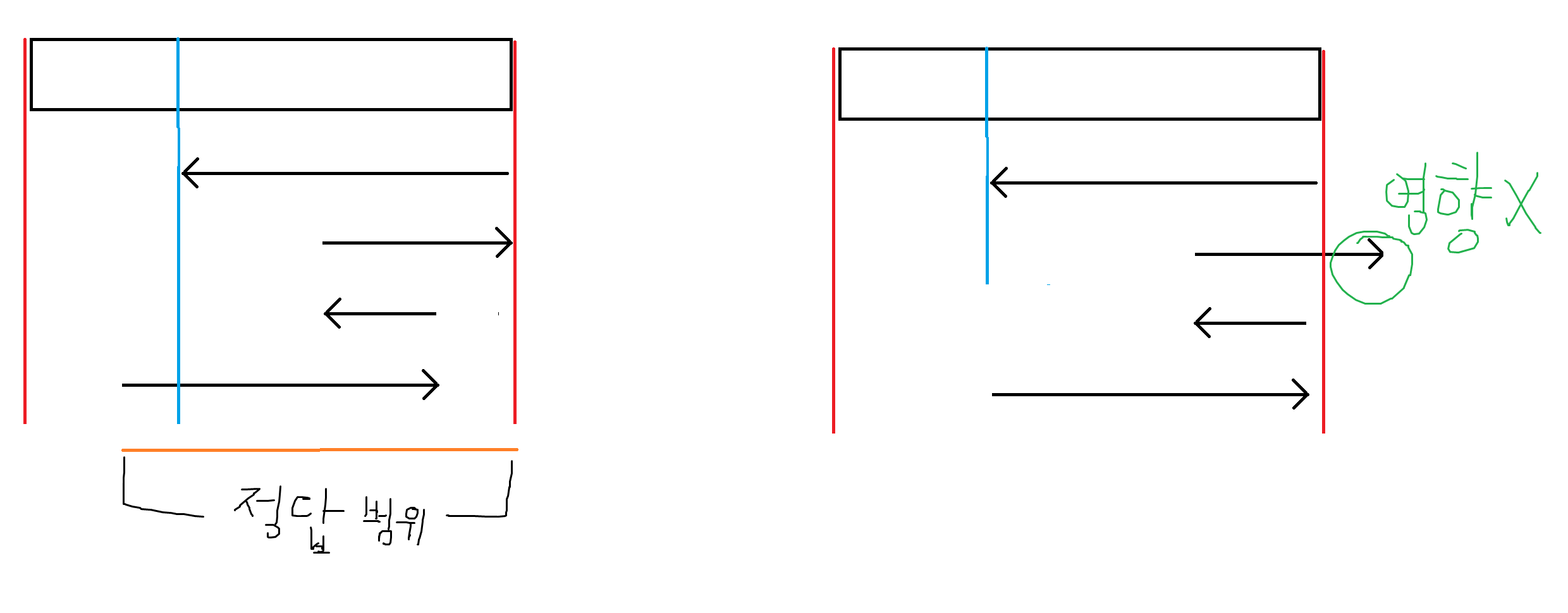
위 그림 처럼 쿼리가 있을 경우 정답 범위는 주황색 부분이다.
정답 범위 안에서 시작점을 오른쪽으로 움직인 경우의 예가 오른쪽 그림이다.
시작점을 오른쪽으로 이동해도 튀어나온 범위는 벽에 막혀 있어서 항상 마지막에 출발하는 쿼리는 벽에서부터 시작한다.
다르게 말하면 왼쪽으로 이동하는 마지막 쿼리가 항상 오른쪽 벽에서 출발한다는 조건을 만족하면 정답이 된다는 뜻이다.
눈치가 빠르다면 보이겠지만 시작점과 벽까지의 거리가 정답 범위이다.
(시작점에서 오른쪽으로 가장 멀리 이동할 수 있는 거리가 벽보다 크거나 같아야 한다는 뜻이다.)

이번에는 시작점이 정답 범위를 벗어난 경우를 생각해보자

시작점을 왼쪽으로 이동했더니 도달하는 좌표가 영향을 받아 왼쪽으로 이동한 모습을 볼 수 있다.
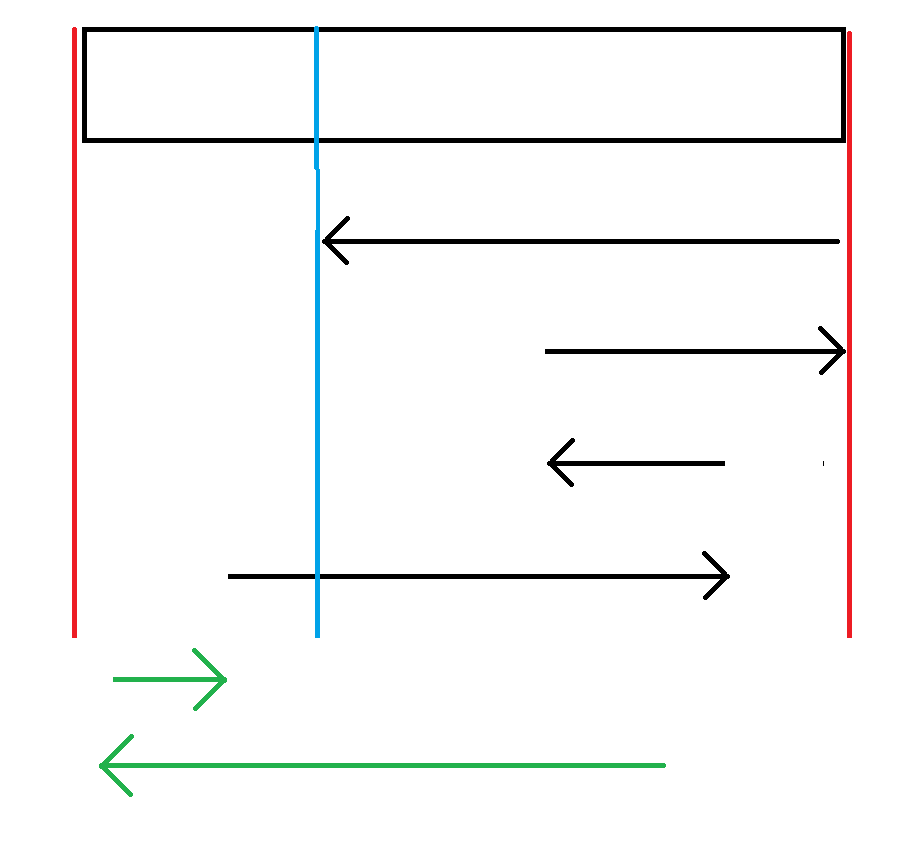
마지막으로 이 그림은 2개의 쿼리가 추가된 그림이다.
이 경우에는 정답의 범위가 어떻게 될까? 양쪽 벽에 맞닿은 적이 있기 때문에 모든 범위에서 정답이 가능하다.
고, 쿼리가 이동했을 때 좌표 범위에서 벗어나면 더 이상 영향을 받지 않고 그 다음 쿼리들은 일정한 모습을 띈다는 사실을 확인했
이전 그림에서 시작점을 이동하면 벽에 닿지 않은 쿼리들이 시작점을 따라 이동하는 모습을 확인했다.
이에 따라 위 그림은 시작점을 어느 방향으로 시작점을 이동해도 쿼리가 벽을 만나 고정이 되므로, 모든 좌표가 가능한 경우다.
계속 벽에 닿았는지 여부를 파악한 이유가 이 때문이다.
아래 그림을 따라 보면서 쿼리를 도착점에서 시작점으로 가는 생각을 해보자.
1번 그림은 쿼리를 거꾸로 진행했을 때 먼저 오른쪽 벽에 닿는다.
이후 왼쪽으로 이동하는데 범위를 벗어났지만, 이미 오른쪽 벽에 닿아 위치가 고정이 되어있기 때문에 왼쪽벽으로 아무리 이동해도 전체 쿼리의 도착점이 변경되지 않는다.
2번 그림은 쿼리를 거꾸로 진행했을 때, 오른쪽 벽에 닿았지만 왼쪽 벽에는 닿지 않았다.
그렇기 때문에 초록색의 범위를 벗어난 쿼리로 인해 도착점이 왼쪽으로 이동하게 되는 모습을 확인할 수 있다.

말로 표현하니 어렵지만 그림을 그려보면서 생각하면 더 이해가 잘 될 것이다.
이제 이를 이용해 벽에 닿았는지 여부로 경우를 나눌 수 있다.
먼저 도착점에서 쿼리를 역행한다.
이때 쿼리가 좌표 범위를 벗어난다면 반대쪽 벽에 닿은 적이 있는지 확인한다.
만약 반대쪽 벽에 닿은 적이 없다면 가능한 경우는 0이다.
만약 반대쪽 벽에 닿은적이 있다면, 이 경우는 모든 범위가 시작점이 될 수 있다. (즉, 양쪽 벽에 닿았다는 뜻)
이번에는 한쪽 벽만 닿는 경우를 생각해보자
이 경우에는 시작점이 될 수 있는 범위가 쿼리를 역행했을 때, 마지막으로 도착한 지점부터 한쪽 벽까지의 거리가 시작점이 될 수 있는 경우다.
ex) 왼쪽 벽이라면 [0 ~ 마지막으로 도착한 지점] , 오른쪽 벽이라면 [마지막으로 도착한 지점 ~ (m or n)]
마지막으로 양쪽 벽에 닿지 않았다면 가능한 시작점은 마지막으로 도착한 지점 1개 뿐이다.
이를 구현해 x좌표와 y좌표의 가능한 시작좌표들을 구하고 정답을 return하면 된다.
[아이디어 정리]
- 도달할 도착점을 기준으로 쿼리를 역으로 진행한다.
- 쿼리를 진행하면서 좌표 범위를 벗어나는지, 벽에 닿았는지 여부를 판단해 시작점의 범위를 구한다.
- x와 y축의 시작점의 범위를 구했다면, 둘을 곱해 정답을 return한다.
Code
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
long long solution(int n, int m, int x, int y, vector<vector<int>> queries) {
long long answer = 0;
// 0은왼, 1은 오, 2는 위, 3은 아래, x는 세로 y는 가로, n은 세로 m은 가로
long long ny=y, nx=x;// 최종적으로 도달하는 상대 좌표를 나타냄
long long tn=n, tm=m, sty,stx; //tm tn은 long long으로 변환한 n, m
vector<int> nq;
bool wL=false,wR=false,wU=false,wD=false; //벽에 닿았는지 판단하는 변수
for (int i=queries.size()-1; i>=0; i--)
{
if (ny==0)
{
wL=true;
}
else if (ny==m-1)
{
wR=true;
}
nq=queries[i];
if (nq[0]==0) //쿼리를 따라 거꾸로 이동 해야한다.
{
ny+=nq[1];
}
else if (nq[0]==1)
{
ny-=nq[1];
}
if (ny<0) //범위를 벗어났을 때 반대쪽 벽에 닿은적이 있는지 판단
{
if (wR) //반대쪽 벽에 닿은적이 있는가?
{
ny=0;
wL=true;
}
else
{
return 0;
}
}
if (ny>m-1) //범위를 벗어났을 때 반대쪽 벽에 닿은적이 있는지 판단
{
if (wL) //반대쪽 벽에 닿은적이 있는가?
{
ny=m-1;
wR=true;
}
else
{
return 0;
}
}
/// x축 확인
if (nx==0)
{
wU=true;
}
else if (nx==n-1)
{
wD=true;
}
if (nq[0]==2) //거꾸로 이동 위 방향 숫자가 감소
{
nx+=nq[1];
}
else if (nq[0]==3)
{
nx-=nq[1];
}
if (nx<0)
{
if (wD)
{
nx=0;
wU=true;
}
else
{
return 0;
}
}
if (nx>n-1)
{
if (wU)
{
nx=n-1;
wD=true;
}
else
{
return 0;
}
}
}
long long xSize=1,ySize=1;
if (wR&&wL)
ySize=m;
else if (wR)
ySize=m-ny;
else if (wL)
ySize=ny+1;
if(wU&&wD)
xSize=n;
else if (wU)
xSize=nx+1;
else if (wD)
xSize=n-nx;
answer=(long long)xSize*ySize;
return answer;
}
+ [풀이 2]
설명은 쿼리를 역행하면서 풀었지만, 쿼리를 순차적으로 실행해서 정답을 구할 수도 있다.
처음 시작점을 0, 0으로 정해 모든 쿼리를 더했을 때, x와 y축 변화량을 계산한다.
이후 x와 y축 변화량을 이용해 시작점을 정한다.
마찬가지로 시작점을 따라가면서 양쪽 벽에 닿았는지 여부를 체크하면서 쿼리를 진행한다.
(이때 좌표 범위를 벗어날 수 없으므로 좌표의 min값은 0, max값은 (m - 1 or n -1)이 된다.)
최종적으로 도달한 좌표가 도착점이 맞다면 벽에 닿았는지 여부로 시작점이 될 수 있는 범위를 계산한다.
(이전 풀이와 똑같이 벽을 기준으로 시작점과 거리를 계산하면 된다.)
Code (쿼리 순행)
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
long long solution(int n, int m, int x, int y, vector<vector<int>> queries) {
long long answer = -1;
// 0은왼, 1은 오, 2는 위, 3은 아래, x는 세로 y는 가로, n은 세로 m은 가로
long long ny=0, dy=0, nx=0,dx=0;// 최종적으로 도달하는 상대 좌표를 나타냄
long long tn=n, tm=m, sty,stx;
vector<int> nq;
for (int i=0; i<queries.size(); i++)
{
nq=queries[i];
if (nq[0]==0)
{
dy-=nq[1];
}
else if (nq[0]==1)
{
dy+=nq[1];
}
}
ny=y-dy;
bool FL=false,FR=false;
if (ny<=0)
{
FL=true;
ny=0;
}
else if (ny>=m-1)
{
FR=true;
ny=m-1;
}
sty=ny;
for (int i=0; i<queries.size(); i++)
{
nq=queries[i];
if (nq[0]==0)
{
ny-=nq[1];
if (ny<=0)
{
FL=true;
ny=0;
}
}
else if (nq[0]==1)
{
ny+=nq[1];
if (ny>=m-1)
{
FR=true;
ny=tm-1;
}
}
}
for (int i=0; i<queries.size(); i++)
{
nq=queries[i];
if (nq[0]==2)
{
dx-=nq[1];
}
else if (nq[0]==3)
{
dx+=nq[1];
}
}
nx=x-dx;
bool FD=false,FU=false;
if (nx<=0)
{
FU=true;
nx=0;
}
else if (nx>=n-1)
{
FD=true;
nx=n-1;
}
stx=nx;
for (int i=0; i<queries.size(); i++)
{
nq=queries[i];
if (nq[0]==2)
{
nx-=nq[1];
if (nx<=0)
{
FU=true;
nx=0;
}
}
else if (nq[0]==3)
{
nx+=nq[1];
if (nx>=tn-1)
{
FD=true;
nx=tn-1;
}
}
}
long long xSize,ySize;
if (nx==x&&ny==y)
{
if (FU&&FD)
{
xSize=tn;
}
else if(FU)
{
xSize=stx+1;
}
else if(FD)
{
xSize=tn-stx;
}
else
{
xSize=1;
}
if (FL&&FR)
{
ySize=tm;
}
else if(FL)
{
ySize=sty+1;
}
else if(FR)
{
ySize=tm-sty;
}
else
{
ySize=1;
}
}
else
{
return 0;
}
answer=xSize*ySize;
return answer;
}
오랜만에 고민이 많이 필요했던 문제였다..
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] 매칭 점수 (2019 KAKAO BLIND RECRUITMENT) (4) | 2024.03.18 |
|---|---|
| [프로그래머스/C++] 호텔 방 배정 (3) | 2024.03.16 |
| [프로그래머스/C++] 스티커 모으기 (0) | 2024.03.14 |
| [프로그래머스/C++] 미로 탈출 명령어 (2023 KAKAO BLIND RECRUITMENT) (0) | 2024.03.13 |
| [프로그래머스/C++] 지형 편집 (2) | 2024.03.11 |