풀이
[문제 풀이]
이 문제를 봤을 때, 블록의 층에 해당하는 높이가 최댓값이라는 사실은 쉽게 추리할 수 있다.
예를 들어 블록의 층이 2층과 4층짜리만 있다고 가정하자.
이 경우 모든 블록을 2층으로 만들거나 4층으로 만들 경우에 답이 있다.
왜냐하면 3층에서 2층으로 만드는 비용을 a라고 하고, 3층에서 4층으로 만드는 비용을 b라고 하자.

그러면 위 그림처럼 4층에서 3층으로 가는 비용도 a로 같다.
그렇기 때문에 a와 b가 대소 관계를 갖게 된다면, 정답은 2층이나 4층에 있게 된다.
(a==b인 경우만 3층일 경우가 정답이 될 수 있는데, 이 경우는 2층으로 쌓나 4층으로 쌓는 경우도 3층으로 쌓는 경우와 비용이 같게 된다.)
이제 이 점에 유의하면서 문제를 풀면 되는데, 모든 층은 최대 300*300개를 가질 수 있다.
그렇기 때문에 각 층을 탐색할 때 마다, 블럭의 층에 대해 계산을 하면 300^4가 돼 시간초과가 된다.
그러므로 각 층에 대해 계산을 할 때 한번에 계산해 시간을 줄이는게 중요하다.
계산의 횟수를 줄이기 위해서 정렬이 필요한데, 정렬을 할 경우 블럭의 높이를 연속적으로 표현할 수 있어 이전 결과값을 이용해 한번에 비용을 계산할 수 있기 때문이다.
아래 그림을 예로 설명을 하면

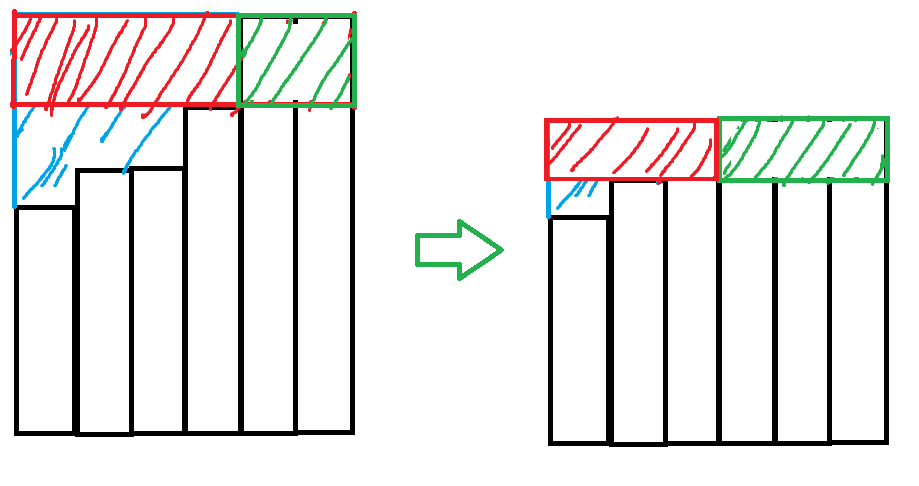
계산을 줄이는 방법은 먼저 모든 층을 가장 높은 층으로 쌓고 비용을 계산한다.
이후 블럭의 높이를 두번째로 높은 층으로 변경한다.
이때, 빨간 부분 만큼의 비용은 필요가 없어졌으므로 빼주고, 초록 부분은 블록을 제거해야하므로 비용에 더해준다.
변경되는 비용을 계산하면
빨간 부분 = (두번재로 높은 층보다 높은 블럭 수) * (이전에 쌓은 블럭 높이 - 다음 층의 높이 차)*P
초록 부분 = (모든 블럭 수 - 두번재로 높은 층보다 높은 블럭 수) * (이전에 쌓은 블럭 높이 - 다음 층의 높이 차)*Q
이제 이 비용을 계산해 더해주면 두번째로 높은 층을 쌓는데 필요한 비용이 계산된다.
마찬가지로 다음 층도 아래 그림처럼 계산을 해주면 된다.
여기서 초록부분의 블럭 수를 계산을 중복으로 하지 않게 주의하고 모든 층의 비용을 계산한 다음 가장 작은 비용을 return하면 된다.
+ 처음에 Map을 이용해 블럭의 수를 저장하고 Map을 정렬해 사용했다. 이 과정에서 효율성 시간 초과가 걸렸는데, 도저히 아이디어가 생각나지 않았다.
문제는 vector를 사용해 정렬하니 바로 통과가 됐는데, 이유를 찾다 보니 아래와 같은 글을 찾을 수 있었다.
정렬 속도 비교
여러가지 언어와 정렬 방법을 이용해서 시간이 얼마나 걸리는지 비교해 보았습니다. 방법: N (= 10,000,000)개의 정수를 입력받은 다음, 오름차순으로 정렬하는 시간을 측정. 10번 측정해서 평균값으
www.acmicpc.net
Map을 sort하는게 생각보다 많이 느려서 같은 풀이방법인데도 시간초과가 났던 것 같다.
[아이디어 정리]
- 블럭을 내림차순으로 정렬한다.
- 가장 높은 층까지 블럭을 쌓고 비용을 계산한다.
- 다음으로 높은 층까지 블럭을 쌓는 비용을 계산하며, 모든 비용을 계산한다.
- 가장 작은 값을 return한다.
Code
#include<vector>
#include<map>
#include<algorithm>
using namespace std;
long long solution(vector<vector<int> > land, int P, int Q) {
// Q는 제거, P는 쌓기
// 정렬 후 쌓는거, 정렬 nLogn으로 계산
map<long long,long long> PM;
int n=land.size();
vector<long long>mV(n*n);
int ss=0;
for (int i=0; i<land.size(); i++)
{
for (int j=0; j<land[0].size(); j++)
{
mV[ss]=land[i][j];
ss++;
}
}
sort(mV.begin(),mV.end(),[](long long a, long long b){return a>b;});
long long stMax=mV[0];
long long retAns=0,minV,nowBlock=0;
for (int i=0; i<n*n; i++)
{
retAns+=(stMax-mV[i])*P;
if (mV[i]==stMax)
{
nowBlock++;
}
}
minV=retAns;
long long block=n*n;
for (int i=nowBlock; i<mV.size(); i++)
{
if (mV[i]==stMax)
{
nowBlock+=1; //다음에 계산할 층보다 높은 블럭 수 미리 계산
}
else
{
retAns+=(stMax-mV[i])*(Q*(nowBlock)-P*(block-nowBlock));
stMax=mV[i];
minV=min(minV,retAns);
nowBlock+=1; //다음에 계산할 층보다 높은 블럭 수 미리 계산
}
}
return minV;
}
Code (Map 사용, 효율성 시간초과)
#include<vector>
#include<map>
#include<algorithm>
using namespace std;
long long solution(vector<vector<int> > land, int P, int Q) {
long long answer = -1;
// Q는 제거, P는 쌓기
// 정렬 후 쌓는거, 정렬 nLogn으로 계산
map<long long,long long> PM;
for (int i=0; i<land.size(); i++)
{
for (int j=0; j<land[0].size(); j++)
{
PM[land[i][j]]+=1;
}
}
vector<pair<long long,long long>> mV(PM.begin(),PM.end());
sort(mV.begin(),mV.end(),[](pair<int,int> a,pair<int,int>b){
return a.first>b.first;
});
long long stMax=mV[0].first;
long long retAns=0,minV, nowBlock=mV[0].second;
for (int i=0; i<mV.size(); i++)
{
retAns+=(stMax-mV[i].first)*mV[i].second*P;
}
minV=retAns;
long long block=land.size()*land.size();
for (int i=1; i<mV.size(); i++)
{
retAns+=Q*(mV[i-1].first-mV[i].first)*nowBlock-P*(mV[i-1].first-mV[i].first)*(block-nowBlock);
nowBlock+=mV[i].second;
minV=min(minV,retAns);
}
return minV;
}
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] 스티커 모으기 (0) | 2024.03.14 |
|---|---|
| [프로그래머스/C++] 미로 탈출 명령어 (2023 KAKAO BLIND RECRUITMENT) (0) | 2024.03.13 |
| [프로그래머스/C++] 아방가르드 타일 (0) | 2024.03.10 |
| [프로그래머스/C++] 등굣길 (1) | 2024.03.08 |
| [프로그래머스/C++] 등산코스 정하기 (2022 KAKAO TECH INTERNSHIP) (0) | 2024.03.07 |