풀이
[문제 풀이]
이 문제를 처음 봤을 때 DP문제면서 매우 간단한 줄 알았다...
하지만 정답이 아니길래 곰곰히 생각해봤더니 많은 패턴들이 숨어있었다.
먼저 아래 그림을 보자
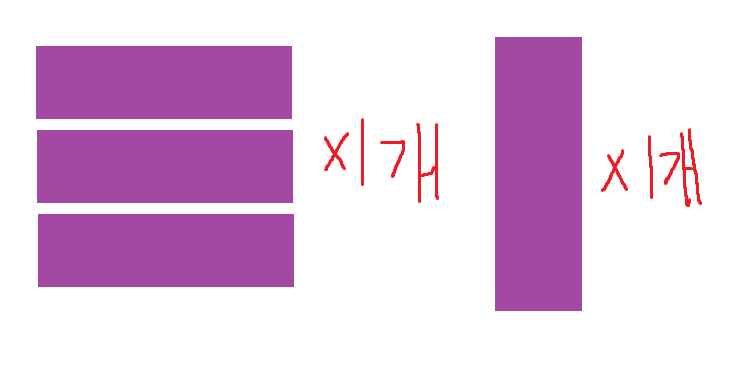
단순히 3개를 연속으로 붙이는 경우와 1개를 붙이는 경우의 패턴이 있다.
저 패턴들을 붙였을 때 길이를 k라고 하면, 아래와 같이 나타낼 수 있다.
$$DP[k-3] \times 1, \,\,\,\,\, DP[k-1] \times 1$$
k보다 길이가 3 짧은 경우에서 3개를 붙여 현재 패턴을 만들 수 있고, k보다 1개 더 길이가 짧은 경우에서 현재 패턴을 만들 수 있기 때문에 위처럼 나타낼 수 있는 것이다.
+ 이러한 타일링 문제를 처음 보면 세워져있는 막대가 2개있는 경우는 왜 없는지 의문이 들 수 있다.

위 그림을 보면 DP[k-1]을 만들 때, DP[k-2]에 막대를 하나 붙인 경우를 포함했으므로, 막대가 2개 있는 경우는 따로 계산하지 않아도 된다.
즉, 이러한 타일링 문제는 이전에 네모를 만드는 경우에서(다른 문제의 해결) 추가로 네모 모양을 붙여 경우를 더하는 문제이므로, 고유한 네모를 만드는 방법이 핵심이다.
고유한 네모를 만드는 방법은 아래와 같다.
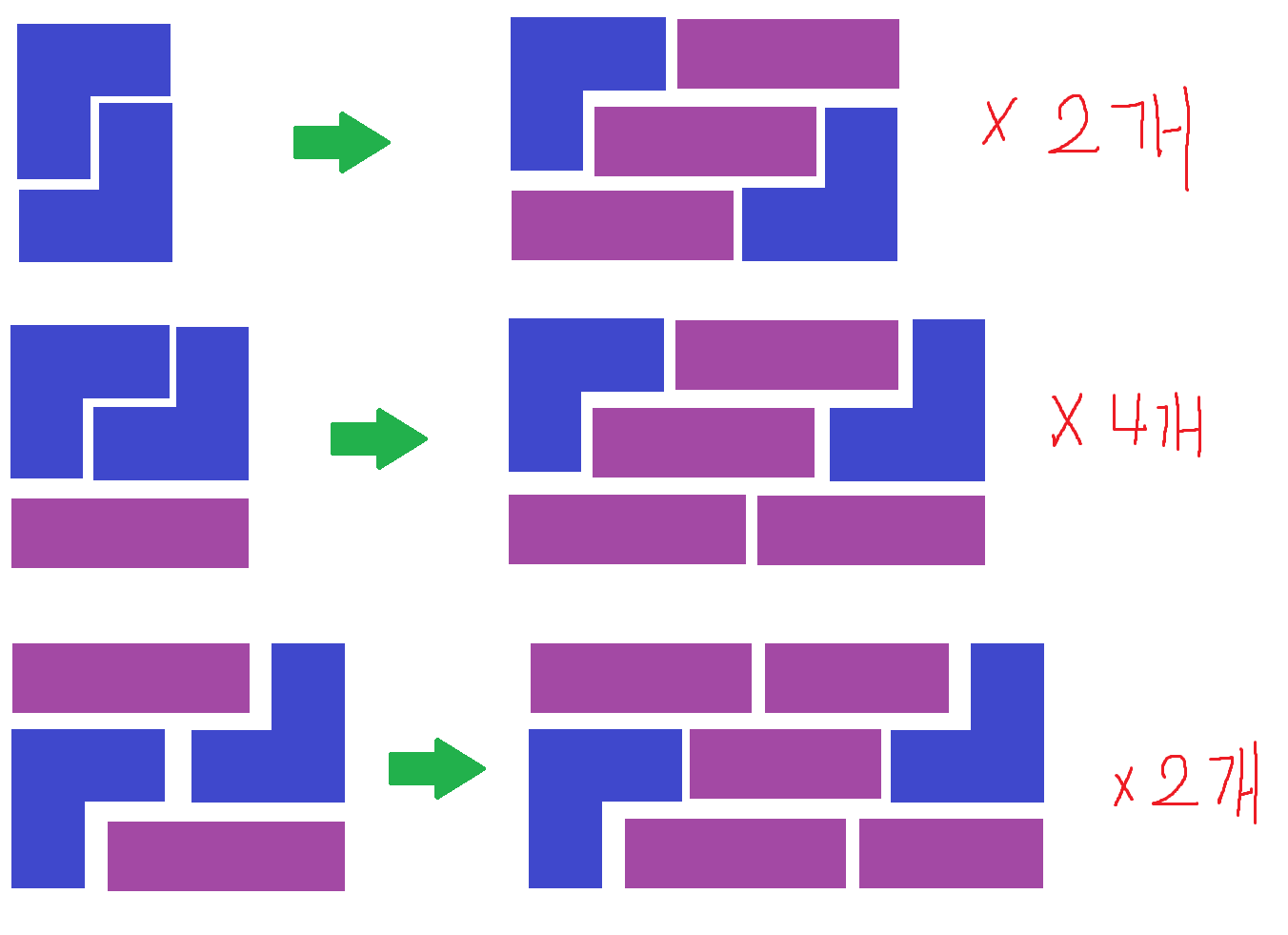
이 문제를 처음에 틀린 이유가 있는데, 위 경우들과 같이 가운데에 가로로 3개 짜리 블럭을 추가하는 경우를 뺐기 때문이었다.
여기서 중요한 점은 그냥 3개를 추가하는 경우를 DP[k-3], DP[k-6], .... 과 같은 식으로 계산을 할 경우 시간 복잡도가 O(n^2)이 돼 시간초과가 된다.
그러므로 이 부분을 잘 계산해야 하는데, 잘 보면 가로로 긴 막대를 3개씩 추가하기 때문에 패턴의 길이가 3씩 늘어나는 모습을 볼 수 있다.
[1] 2, 5, 8, ... , 2 + (3*n)의 모양
[2] 3, 6, 9, ... , 3 + (3*n)의 모양
[3] 4, 7, 10, ... , 4 + (3*n)의 모양
그러므로 이를 활용하면 아래 그림과 같이 계산을 줄일 수 있다.

위 그림은 길이를 3으로 나누었을 때, 2가 되는 사각형을 추가하는 경우들이다.
그러므로 DP[k-2]+DP[k-5]+.... DP[k-(2+3*n)]의 누적합을 알고 있다면,
(DP[k-2]하위의 누적합) * 2(길이를 3으로 나누었을 때, 2가 되는 사각형의 모양)로 한번에 계산할 수 있게 된다.
그래서 누적합을 이용하기 위해 vector를 하나 더 만들고, 누적합[k] = 누적합[k-3] + DP[k]로 저장해 사용했다.
마찬가지로 다른 사각형도 계산을 하면,
DP[k] = DP[k-1] + DP[k-3] + 누적합[k-2]*2 + 누적합[k-3]*4 + 누적합[k-4]*2 로 한번에 계산할 수 있다.
[아이디어 정리]
- 이전에 만들었던 사각형에 일정한 길이의 사각형을 추가하면 더 긴 길이의 사각형을 만들 수 있으므로 DP로 해결할 수 있다.
- DP값을 저장할 vector를 만든다.
- 사각형의 모양이 많으므로 누적합을 이용해 계산을 줄일 vector를 만든다.
- DP의 계산에 누적합을 더해 길이 n의 사각형의 경우의 수를 계산하고, 1000000007로 나누어 나머지를 return한다.
Code
#include <string>
#include <vector>
using namespace std;
const long long Mod=1000000007;
int solution(int n) {
// 1개 추가하는 경우, 3개만 추가하는 경우, (2, 3, 4+ 특이케이스들)
vector<long long> DP(100001,0);
vector<long long> nuDP(100001,0);
DP[0]=1,DP[1]=1; DP[2]=3,DP[3]=10;//
nuDP[0]=1,nuDP[1]=1; nuDP[2]=3, nuDP[3]=11;//
for (int i=4; i<n+1; i++)
{
DP[i]=DP[i-1]+DP[i-3];
DP[i]+=nuDP[i-3]*4;
DP[i]+=nuDP[i-4]*2;
DP[i]+=nuDP[i-2]*2;
DP[i]%=Mod;
nuDP[i]=nuDP[i-3]+DP[i];
nuDP[i]%=Mod;
}
return (DP[n]%Mod);
}
https://school.programmers.co.kr/learn/courses/30/lessons/181186?language=cpp
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] 미로 탈출 명령어 (2023 KAKAO BLIND RECRUITMENT) (0) | 2024.03.13 |
|---|---|
| [프로그래머스/C++] 지형 편집 (2) | 2024.03.11 |
| [프로그래머스/C++] 등굣길 (1) | 2024.03.08 |
| [프로그래머스/C++] 등산코스 정하기 (2022 KAKAO TECH INTERNSHIP) (0) | 2024.03.07 |
| [프로그래머스/C++] 숫자 타자 대회 (1) | 2024.03.06 |