풀이
처음에 이 문제를 봤을 때, 적당히 잘 자른다음 옆으로 밀면서 비교하면 되지 않을까?라고 생각했다.
그런데 옆으로 밀면서 비교해도 특수한 경우가 있어서, 단순 비교로는 풀 수 없을 것이라 생각하고 다른 사람의 힌트를 참고 했다.
알고보니 풀이는 비슷한데 숫자의 개수가 홀수인 경우와 짝수인 경우를 구분해서 생각해야했다.
나는 계속 홀수개의 숫자에서 고민을 하다보니 어려웠던 것이다...
[문제 풀이]
먼저 숫자가 짝수개일 때는 정렬을 한 다음 절반을 나눠서 비교하면 된다.
[짝수일 경우]
아래 그림과 같이 한 다음 숫자의 배치를 b1, a1, b2, a2 순서로 배치한다.

여기서 a1을 먼저 배치하지 않고 b1을 배치하는 이유는 다음과 같다.
a1, b1, a2, b2 순서와 b1, a1, b2, a2 순서를 비교해보자
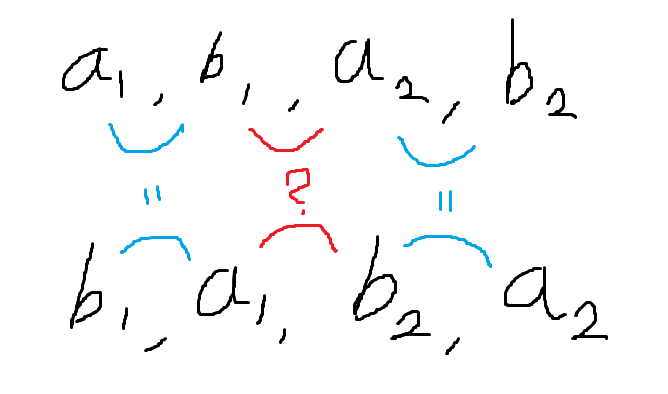
[a1, b1], [a2, b2]를 비교하는 부분은 높이 차이가 같지만, 그 사이의 [b1, a2] 부분과 [a1, b2] 부분이 다르다.
$$b_1 \leq b_2, \quad a_1 \leq a_2 \quad \text{이므로} \quad b_1 - a_2 \leq b_2 - a_1 \quad \text{이다.} $$
그러므로 b1을 먼저 배치하는게 더 높이 차가 크게 된다.
그러면 여기서 왜 절반을 나누고 이렇게 배치하는게 높이차의 최솟값의 최대값을 구하는 방법일까?
만약 이러한 형태가 아닌 무작위로 배치를 했다고 가정하자.
아래 그림과 같이 무작위로 숫자를 배치하면 처음에 나온 수들의 차는 더 클 수 있다.
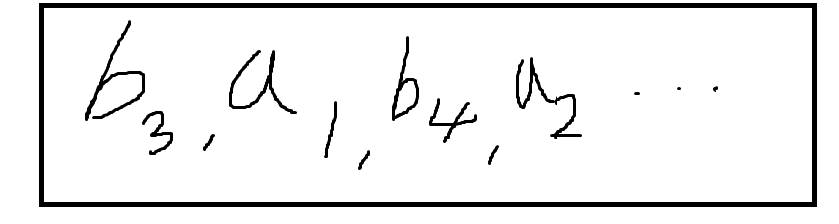
하지만 사용하지 않은 b1과 b2가 존재한다. 이 때 b1, b2 숫자들이 a3이나 a4와 같이 더 큰 숫자와 붙으면 높이차의 최솟값의 최댓값이 줄어들게 된다.
그러므로 b1과 b2는 a에 붙을 경우 절반을 나누고 배치하는 경우보다 높이차의 최솟값의 최댓값이 줄어들기 때문에 다른 숫자에 붙어야 된다.
위에서 b1과 b2를 a에 붙일 수 없다는 사실을 알았으니 b에 붙여보자. b1, b2와 차이가 많이 나 붙여도 되는 b5와 b6이 존재한다고 가정하자
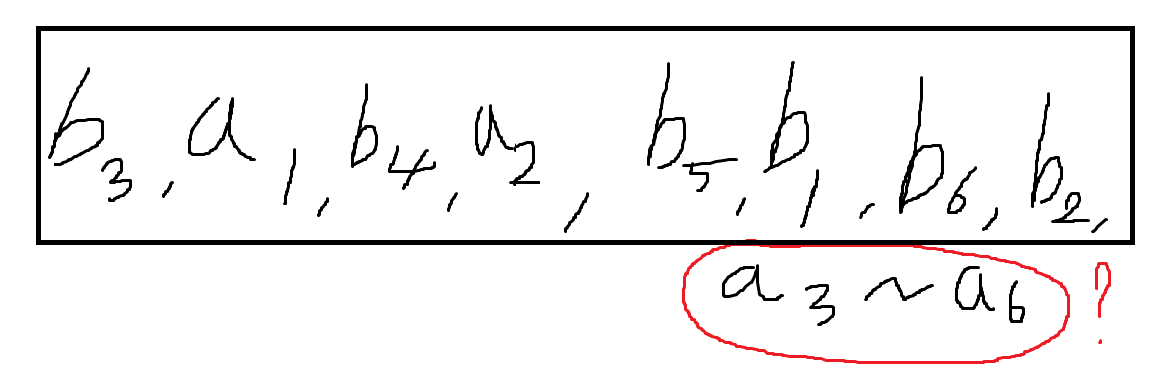
마찬가지로 위와 같이 배치할 수 있겠지만, 이후 남는 a3~a6의 숫자들은 서로 붙을 수 밖에 없다.
왜냐하면 b의 개수와 a의 개수가 같은데 b와 b가 붙었으므로 a와 a가 붙는 경우도 나올 수 밖에 없기 때문이다.
그렇기 때문에 a<=b라는 정의에 의해서 a끼리 붙는 경우가 생겨 높이차의 최솟값의 최댓값이 작아지게 된다.
$$a\leq b \quad \text{이므로,} \quad a_n-a_m\leq b_1-a_m \text{는 항상 성립한다.}$$
짝수인 경우는 위와 같이 논리적으로 생각하면 쉽게 구할 수 있는데, 홀수일 경우는 약간 다르다.
[홀수일 경우]
이 경우에는 다음과 같이 나눈다.
정렬을 한 다음 가장 큰 수를 제외하고 절반으로 나눠 a와 b로 구간을 나눈다음 짝수를 배치할 때와 마찬가지로 배치한다.
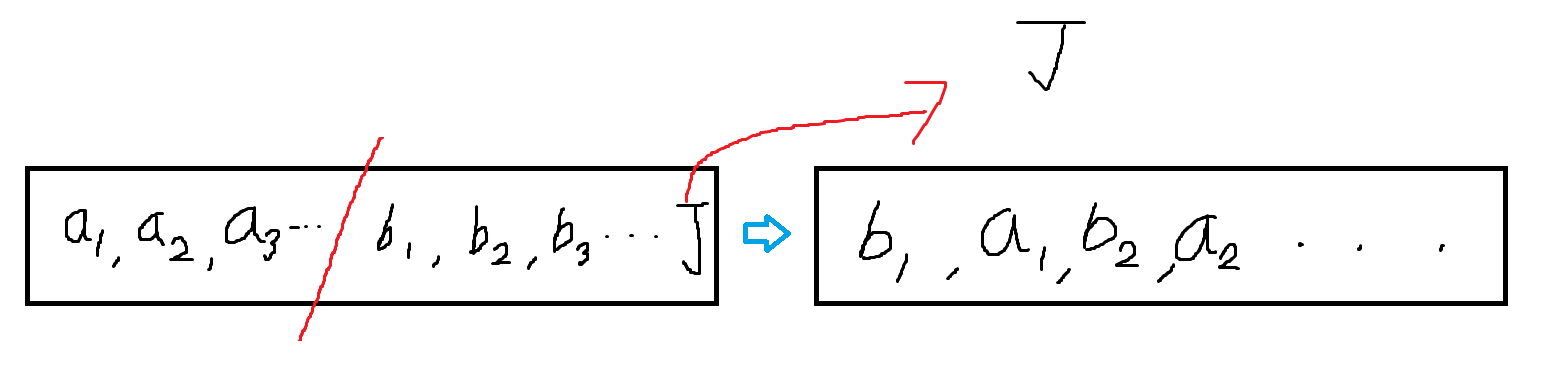
(가장 큰 수 대신 가장 작은 수를 빼고 절반으로 나눠도 되지만 편의상 큰 수로 진행)
이후가 짝수와 차이가 나는데, 위 경우에서 임의의 bm am 위치의 차이가 가장 차이가 작다고 가정해 보자.
이 경우 J를 이용해서 차이를 줄일 수 있다.
아래와 같이 배치되어 있는 숫자들을 옆으로 밀어서 bm을 맨뒤로 보낸다.

이렇게 옆으로 밀 경우 an과 b1이 붙게 되는데 an과 b1은 정렬했을 때 바로 옆에 있는 수 이므로, 크기 차이가 작게 되는 부분이다. 이 부분에 J를 삽입해 an과 b1의 차이가 아닌 an과 J, b1과 J의 차이로 바꿔 주면 된다.
이렇게 바꿀 경우 J와 b1의 차이를 비교해야한다. 차이가 가장 작았던 am과 bm을 쪼갰으므로 J-b1의 차이와 두번째로 차이가 작은 수를 비교해서 더 작은 수를 return 하면 된다.
(J-an은 고려할 필요가 없는 이유는 an<=b1, bn-an<=J-an의 두 경우가 있기 때문이다.)
여기서 예외가 발생할 수 있는데 만약 J와 b1의 차이가 앞에서 구한 bm-am보다 작을 수 있다는 것이다.
그렇다면 이 경우는 아래와 같이 배치하고, bm-am이 최솟값이 된다.
(가정에 의해 bn-an<=J-an, 이고 bm-am이 최솟값이였기 때문)

즉, 위 과정을 요약하면 J-b1과 [b1, a1, ... bn, an]의 최솟값 들을 비교하면 된다는 결론이 나온다
이를 더 편하게 계산하려면 J를 맨앞에 두고 배열을 만든다.

그리고 높이의 차이를 계산한다.
여기서 계산한 높이의 차이를 다시 정렬하고 두번째로 작은 값을 return하면 된다.
왜냐하면 가장 작은 값은 배열을 옆으로 밀어 제거할 수 있기 때문이다.
+ 추가
이 과정에서 b1-a1, b2-a2 들만 계산하면 된다.

b1-a1보다 b2-a1의 높이 차이가 큰 것은 당연하기 때문이다. (정렬했으므로)
홀수일 경우도 마찬가지다.
*만약 b1-a1, b2-a1의 차가 최솟값이고 R로 같을 경우에도 b2-a1값은 배열에 추가하지 않아도 된다.
왜냐하면 정렬했기 때문에 a2>=a1인데 b1-a1=b2-a1이라면, b1=b2가 된다.
여기서 b2-a2의 차이도 있는데, b1-a1의 차이가 최소라면 b2-a2>=b1-a1=b2-a1, 이 되고 a1<=a2이므로 위 가정을 만족하는 a2는 a1과 같게 되기 때문에 b1-a1=b2-a2가 되어 b2-a1을 계산할 필요가 없기 때문이다
배열에 b1-a1, b2-a2값이 추가되어 어차피 2번째 최소값은 b1-a1과 같은 값이 return 된다.
[아이디어 정리]
- heights의 개수가 홀수일 경우와 짝수일 경우로 나눈다.
- 짝수일 경우 정렬한 뒤 절반으로 나눈다. (큰 부분은 b, 작은 부분은 a)
- b1-a1, b2-a2, ... bn-an을 전부 계산한 다음 가장 작은 수를 return한다.
- 홀수일 경우 정렬한 뒤 가장 큰 수를 제외하고 절반으로 나눈다.
- b1-a1, b2-a2, ... bn-an, J-b1을 전부 계산한 다음 두번째로 작은 수를 return한다.
Code
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<int> heights) {
sort(heights.begin(),heights.end());
vector<int> minusV;
if (heights.size()%2==1) //홀수
{
for (int i=0; i<heights.size()/2; i++)
{
minusV.push_back(heights[i+heights.size()/2]-heights[i]);
}
minusV.push_back(heights[heights.size()-1]-heights[heights.size()/2]);
sort(minusV.begin(),minusV.end());
return minusV[1];
}
else
{
for (int i=0; i<heights.size()/2; i++)
{
minusV.push_back(heights[i+heights.size()/2]-heights[i]);
}
sort(minusV.begin(),minusV.end());
return minusV[0];
}
return 0;
}
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] 보행자 천국 (2017 카카오코드 예선) (0) | 2024.02.04 |
|---|---|
| [프로그래머스/C++] N으로 표현 (0) | 2024.02.02 |
| [프로그래머스/C++] 가장 긴 팰린드롬 (feat. Manacher's Algorithm) (0) | 2024.02.01 |
| [프로그래머스/C++] 카운트 다운 (0) | 2024.01.31 |
| [프로그래머스/C++] 스타 수열 (1) | 2024.01.31 |