풀이
[문제 풀이]
이 문제를 보자마자 O(n^2)으로 해결 되겠다고 생각이 들었다. 문자열의 사이즈가 작았기 때문이다.
하지만 더 효율적인 알고리즘이 뭐가 있을까 찾아보다가
Manacher's Algorithm을 알게 됐다.
Manacher's Algorithm을 처음 봤을 때, 설명이 많이 복잡하다는 생각이 들었다.
[참고]
https://m.blog.naver.com/jqkt15/222108415284
즉 Manacher's Algorithm을 요약하면 이전에 Palindrome인지 체크한 것을 이용한 것이다.
for문으로 앞에서 부터 문자열이 Palindrome인지 체크하는데, 이때 Palindrome이라면 Palindrome의 범위가 얼마인지 저장해 두는 것이다.
i번째 문자를 중심으로 몇 칸 떨어진 문자까지 Palindrome인지를 나타낼 때, 칸을 R이라고 하자.
그러면 이 때, i ~ [i+R]번째 문자 사이의 문자를 중심으로 하는 Palindrome을 체크할 때는 하나씩 체크할 필요가 없는 것이다.
왜냐하면 for문으로 앞에서부터 Palindrome을 체크했고, 현재 문자가 i 문자를 기준으로 하는 Palindrom의 범위 안에 있다면, 대칭을 이루어야 하므로 이전에 체크한 Palindrome을 이용할 수 있는 것이다.
예를 들어 i번째 문자가 좌우로 15칸씩 Palindrome을 이룬다고 가정하자.
그러면 i+10번째 문자와 i-10번째 문자는 서로 대칭이므로 i+3번째 문자는 i-3번째 문자의 Palindrome 범위를 이용할 수 있는 것이다.
그림으로 보면

i-10과 i+10은 대칭이므로 i+10의 Palindrome은 i-10의 Palindrome을 이용할 수 있다.
이때, 중요한 것은 i+15범위 까지의 Palindrome 여부만 알 수 있다는 것이다.
i-10의 Palindrome 범위가 5칸이내라면 마찬가지로 i+10의 Palindrome 범위도 i-10과 같을 것이다.
이 때, 만약 i-10의 Palinrome의 범위가 i+15까지라면 어떻게 될까?

아래 그림에서 본 것과 같이 i+10을 기준으로 Palindrome을 이루는 부분은 최소 i-10과 범위가 같을 것이다. (대칭이므로)
그렇기 때문에 i+10을 기준으로 Palindrome을 이루는 부분은 최소 i-10과 같을 것이며, 이후에 더 Palindrome이 길어질 수 있는지 비교를 통해 확인해 봐야한다. (i+15를 넘어가는 범위는 대칭인지 모르기 때문이다.)
여기서 만약 i-10의 Palindrome범위가 i-15를 넘어서는 범위를 포함하고 있었다면 어떻게 될까?
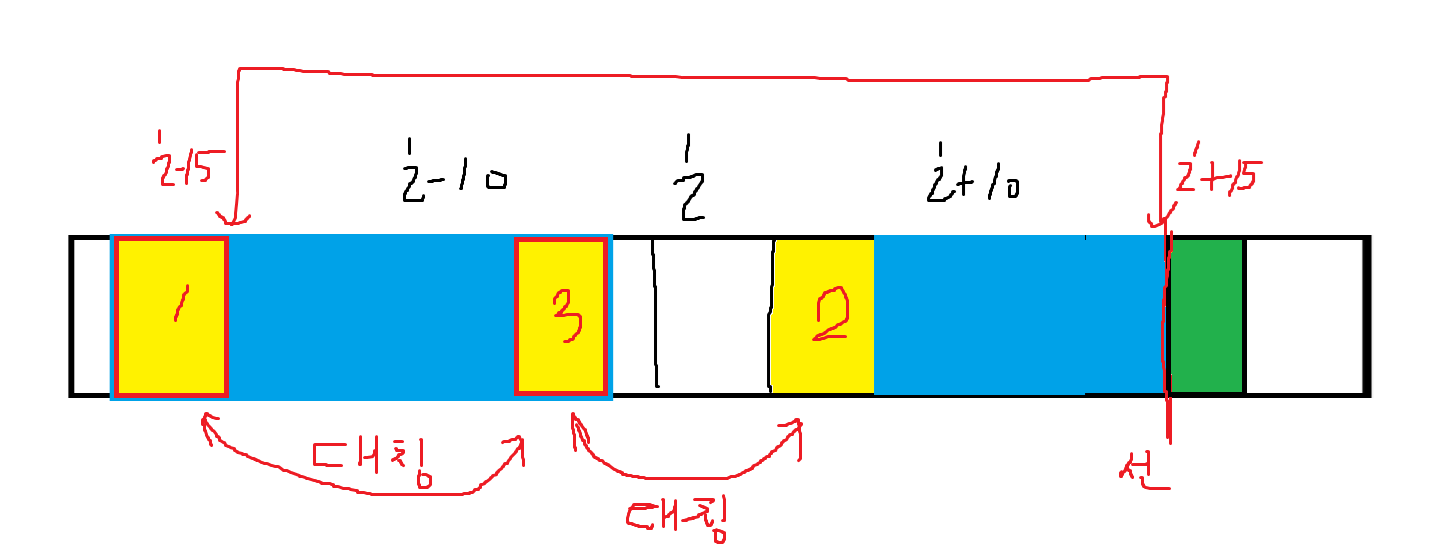
이 경우에는 Palindrome의 범위가 i+10을 기준으로 한 Palindrome은 i+15범위를 넘지 않는다.
왜냐하면 i-10에서는 Palindrome의 범위가 i-15를 넘어갔는데, 만약 i+10을 기준으로 한 Palindrome이 i+15를 넘어가려면
애초에 i를 기준으로 한 Palindrome도 범위가 15보다 넓어졌을 것이기 때문이다.
그림에서 3번과 2번의 노란 부분은 대칭인 부분이고, 만약 i+10을 기준으로 Palindrome의 범위가 i+15를 넘어간다면 초록색 부분도 2번 부분과 대칭인 부분이 있어야 하기 때문이다.
그런데 그렇게 된다면 1번부분과도 초록색 부분은 대칭인 부분이 생기게 되어 i를 기준으로 한 Palindrome의 범위가 15를 넘는다는 뜻이므로, i를 기준으로 Palindrome이 15라는 가정에 위배되기 때문이다.
그래서 이 경우에는 i+10을 기준으로 한 Palindrome이 i+15범위를 넘지 않는다.
위와 같이 Manacher's Algorithm을 이용하면 O(N)의 시간복잡도로 문제를 해결할 수 있게 된다.
[아이디어 정리]
- for문으로 Palindrome인지 체크를 한다.
- 현재 index가 이전 문자를 중심으로 한 Palindrome의 범위에 포함된다면, 대칭을 이용해 반대편 문자를 중심으로 한 Palindrome의 범위를 이용해 현재 문자가 얼마나 긴 Palindrome을 만들 수 있는지 빠르게 체크한다.
- 이 때, Manacher's Algorithm은 한 문자가 중심이 되는 Palindrome을 구하기 때문에 문자열 사이에 #을 넣어 홀수 문자열의 Palindrome이 이루어지게 변형해서 문제를 해결한다.
Code
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int solution(string s)
{
int answer=0;
string realS="#";
for (int i=0; i<s.length(); i++)
{
realS+=s[i];
realS+='#';
}
// [실행] 버튼을 누르면 출력 값을 볼 수 있습니다.
vector<int> Palin(realS.length(),0); // palin값
vector<int> Centre(realS.length(),0); // centre값
vector<int> Radius(realS.length(),0); // R값
int nowP=0,R=0,nowC=0,maxR=1;
for (int i = 1; i<realS.length(); i++)
{
if (nowP<i)
{
R=0;
}
else
{
R=min(nowP-i,Radius[nowC*2-i]);
}
while(i-R-1>=0&&i+R+1<realS.length()&&realS[i-R-1]==realS[i+R+1])
{
R++;
}
Radius[i]=R;
if (nowP<i+Radius[i])
{
nowP=i+Radius[i];
nowC=i;
}
Palin[i]=nowP;
Centre[i]=nowC;
if (maxR<R)
maxR=R;
}
return maxR;
}
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] N으로 표현 (0) | 2024.02.02 |
|---|---|
| [프로그래머스/C++] 재밌는 레이싱 경기장 설계하기 (2023 현대모비스 알고리즘 경진대회 본선) (0) | 2024.02.02 |
| [프로그래머스/C++] 카운트 다운 (0) | 2024.01.31 |
| [프로그래머스/C++] 스타 수열 (1) | 2024.01.31 |
| [프로그래머스/C++] 파괴되지 않은 건물 (2022 KAKAO BLIND RECRUITMENT) (1) | 2024.01.29 |