풀이
[문제 풀이]
이 문제는 조건을 파악하면 빠르게 풀 수 있는 문제다.
구간은 [머리, 가슴, 배] 이며 조건은 (머리 구간 합<배 구간 합< 가슴 구간 합) 을 만족하면 된다.
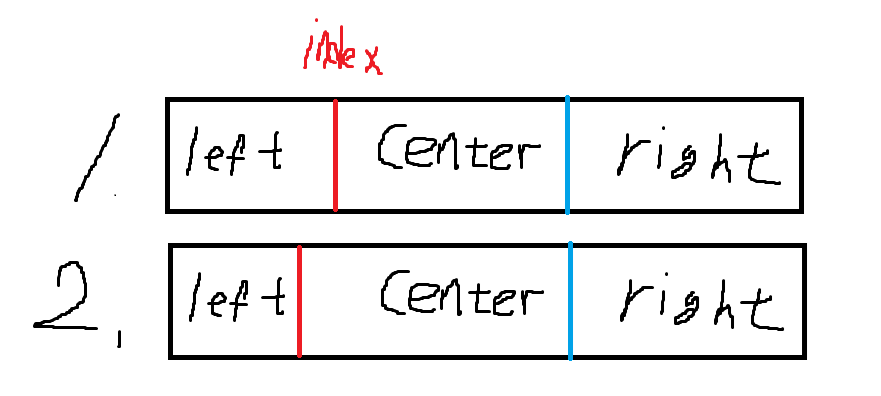
그럼 구간을 크게 [LEFT, CENTER, RIGHT] 로 나눌 수 있다.
이제 이를 이용해 문제를 풀 수 있는데, RIGHT 구간의 값이 정해졌을 때, CENTER의 값이 RIGHT보다 크면서 LEFT 구간이 RIGHT 구간보다 작도록 만족하는 구간 중 가장 큰 인덱스를 찾으면 된다.
즉 그림을 참고하면

위 그림과 같이 표현할 수 있는데 조건을 만족하면서 가장 큰 index를 찾으면 index의 값이 경우의 수라는 사실을 알 수 있다.
왜냐하면 right구간의 값이 정해졌을 때, 조건을 만족하는 가장 큰 index i를 찾았다고 가정해보자
그러면 index i보다 작은 경우에도 항상 조건을 만족하므로 index의 값이 경우의 수가 되는 것이다
(아래 그림을 참고하면 이해가 잘 될 것이다)
이제 index를 찾는 방법을 생각하면 되는데 빠르게 찾기 위해 구간합을 계산하고 이분탐색을 이용해 조건을 만족하도록 분리하는 index를 찾으면 Log(N)의 시간복잡도로 탐색이 가능하다.
그러므로 right의 크기에 따라 조건을 만족하는 가장 큰 index를 찾도록 문제를 풀면 시간복잡도 nLog(n)으로 문제를 해결할 수 있다.
[아이디어 정리]
- 구간 합을 구한다.
- right 구간의 크기를 변경해 나가며 left<right<center 조건을 만족하는 index를 찾는다.
- 이때, index는 이분탐색과 구간합을 이용해 조건을 만족하는 가장 큰 index를 찾는다.
- 찾은 index의 값이 경우의 수 이므로 경우의 수를 더해 결과를 출력한다.
Code
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int findC(vector<long long> &nuH, int ED, long long rS)
{
if (rS>=nuH[ED])
{
return 0;
}
int st = 0, ed=ED-1, mid, ans=0;
long long S = nuH[ed];
while(st<=ed)
{
mid = (st + ed) / 2;
if (nuH[mid]<rS && S-nuH[mid]>rS)
{
ans = mid;
st = mid + 1;
}
else
{
ed = mid - 1;
}
}
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
int N;
cin >> N;
// 머리 가슴 배
// 가슴>배>머리
vector<long long> v(N+1);
vector<long long> nuH(N + 1,0);
for (int i = 1; i <= N; i++) {
cin >> v[i];
nuH[i] = nuH[i - 1] + v[i];
}
long long ans = 0;
for (int i = N; i >= 1; i--) {
ans+=findC(nuH, i, nuH[N] - nuH[i-1]);
}
cout << ans;
return 0;
}
처음에 이분탐색으로 문제를 푸는데 이분탐색 비교 조건에 = 을 빼먹어서 틀렸었다...
실수로라도 빼먹지 않게 조심하자
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 도미노 예측 (No. 17943) (0) | 2024.11.07 |
|---|---|
| [백준/C++] 도로 네트워크 (No. 3176) (0) | 2024.11.05 |
| [백준/C++] 조 짜기 (No. 2229) (0) | 2024.10.29 |
| [백준/C++] Tree (No. 13244) (0) | 2024.10.28 |
| [백준/C++] 규칙적인 보스돌이 (No. 29792) (2) | 2024.10.24 |