풀이
[문제 풀이]
이 문제는 그리디하게 풀 수 있는 문제다.
문제의 조건에서 한번 들린 초콜릿 가게는 다시 들릴 수 없으며, 출발점과 도착점이 정해져있다.
이를 이용하면 초콜릿 가게를 어떤 순서로 방문할지 쉽게 파악할 수 있다.
왜냐하면 최종적으로 초콜릿 맛의 점수가 가장 높도록 방문할 경우 점수가 가장 높은 값만 구하면 되기 때문이다.

위 그림을 보면 S에서 E로 도착하기 위해서는 보라색 구간은 필수로 지나야하는 구간이다.
반면, S의 왼쪽과 E의 오른쪽은 지나도 되고 지나가지 않아도 되는 구간이다.
이를 이용하면 S의 왼쪽 구간의 점수가 0보다 작다면, 굳이 방문할 필요가 없는 구간이다.
마찬가지로 E의 오른쪽 구간도 점수가 0보다 작다면, 굳이 방문할 필요가 없는 구간이다.
그리고 추가로 생각해보면 왼쪽의 가게들을 들리게 되면 S의 아래 가게는 무조건 방문하게 된다.

그러므로 왼쪽을 방문하는 경우에 S의 아래를 무조건 방문한다는는 점을 고려해 방문할지를 판단 하면 된다.
E의 오른쪽 구간도 마찬가지다.
오른쪽 구간을 거쳐서 최종 도착지인 E에 방문해야 하기 때문에 마찬가지로 E의 위쪽 지점을 무조건 거치게 된다.
그러므로 오른쪽 구간을 방문하는 경우 이를 고려해야한다.
그러면 왼쪽 구간과 오른쪽 구간의 초콜릿 가게 점수는 어떻게 계산할까?
계산하는 방법은 간단하다.
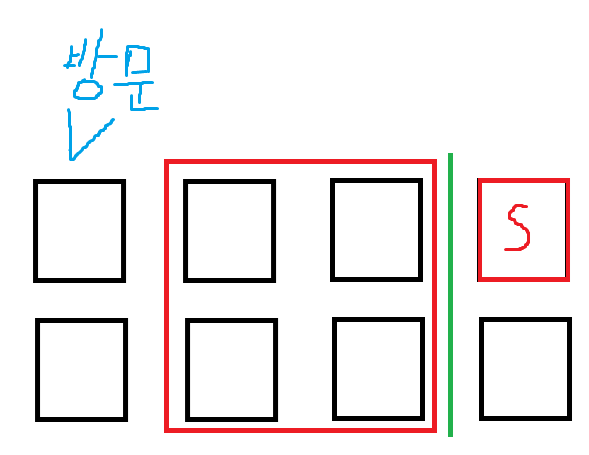
파란색 구간의 초콜릿 집을 방문하면 그 사이에 있는 빨간색 네모안의 초콜릿 가게는 전부 방문하게 된다.
반면 파란색 구간의 아래 초콜릿 집은 방문해도 되고 방문을 하지 않아도 된다.
이를 고려해 i번째 구간의 초콜릿 가게를 방문하면 그 사이의 i ~ s구간 초콜릿집은 전부 방문해야 한다는 점을 알았으므로 S의 왼쪽으로 나아가면서 어느 구간까지 방문하는 경우에 왼쪽 구간의 초콜릿 점수가 최대인지 계산하면 된다.
만약 왼쪽으로 방문하는 경우가 손해라면 방문하지 않으면 된다.
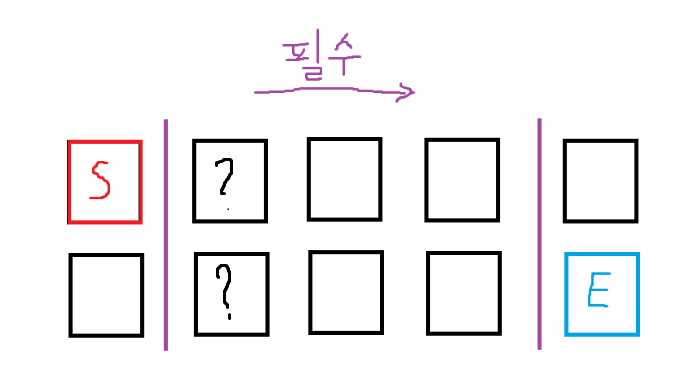
필수인 구간도 마찬가지다.
S에서 시작해 E로 가는 길에서 위 아래 두 개의 초콜릿 가게를 전부 방문해도 되며, 하나만 방문해도 된다.
만약 초콜릿 가게의 점수가 +라면 두 초콜릿 가게를 방문하는게 이득이지만, 초콜릿 가게의 점수가 -라면 그 가게는 방문하지 않는게 이득이다.
그러므로 이러한 점을 고려해 가운데 이동하는 구간을 고려하면 최대 초콜릿 점수를 계산할 수 있다.
[아이디어 정리]
- 초콜릿 가게의 구간을 왼쪽, 가운데, 오른쪽 세 구간으로 나눈다.
- 만약 왼쪽이나 오른쪽으로 이동했다가 돌아오는 경우가 이득이라면 점수를 더한다.
- S에서 출발해 E로 도착하기 위해서 가운데 구간은 적어도 위 아래 하나의 초콜릿 가게를 방문해야한다.
- 그러므로 초콜릿 가게의 점수를 고려해 위, 아래 초콜릿 가게를 전부 방문할지 하나만 방문할지 계산해 이동한다.
Code
#include <iostream>
#include <string>
#include <vector>
#include <cmath>
#include <set>
#include <algorithm>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int T;
cin >> T;
for (int i = 0; i < T; i++)
{
int N;
cin >> N;
vector<vector<long long>> V(2, vector<long long>(N,0));
for (int i = 0; i < N; i++)
cin >> V[0][i];
for (int i = 0; i < N; i++)
cin >> V[1][i];
int a, b, c, d;
cin >> a >> b >> c >> d;
a -= 1, b -= 1, c -= 1, d -= 1;
int tmp;
if (a > c) {
tmp = a, a = c, c = tmp;
tmp = b, b = d, d = tmp;
}
// 왼쪽, 오른쪽, 가운데의 최대 값을 계산한다.
// 왼쪽
long long leftMax=0, rightMax=0;
long long nowMax = 0;
for (int i = a-1; i >=0; i--) {
nowMax += max(V[1][i], V[0][i]);
leftMax = max(nowMax, leftMax);
nowMax += min(V[1][i], V[0][i]);
leftMax = max(nowMax, leftMax);
}
nowMax = 0, rightMax = 0;
for (int i = c + 1; i < N; i++) {
nowMax += max(V[1][i], V[0][i]);
rightMax = max(nowMax, rightMax);
nowMax += min(V[1][i], V[0][i]);
rightMax = max(nowMax, rightMax);
}
long long Ans;
if (a == c) {
// 가운데가 없음.
Ans = V[1][a] + V[0][a];
cout << max(Ans + leftMax, Ans + rightMax) << "\n";
}
else
{
long long midMax = 0;
for (int i = a + 1; i < c; i++) {
midMax += max(V[1][i], V[0][i]);
if (min(V[1][i], V[0][i]) > 0) {
midMax += min(V[1][i], V[0][i]);
}
}
Ans = max(V[b][a], V[0][a] + V[1][a] + leftMax);
Ans += midMax;
Ans += max(V[d][c], V[0][c] + V[1][c] + rightMax);
cout << Ans << "\n";
}
}
}
예전에 똑같은 아이디어로 코드를 구현했는데 틀렸었다
그러네 이번에 다시 똑같은 아이디어로 코드를 구현하니 정답 처리가 됐다
아마 고려하지 않거나 빼먹은 경우가 있었던 것 같다;;
https://www.acmicpc.net/problem/31461
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 외판원 순회 (No. 2098) (1) | 2024.06.24 |
|---|---|
| [백준/C++] 집합 (No. 11723) (0) | 2024.06.23 |
| [C++/백준] 두 원 (No. 7869) (0) | 2024.06.20 |
| [백준/C++] 선분 그룹 (No. 2162) (0) | 2024.06.19 |
| [백준/C++] 집으로 (No. 1069) (0) | 2024.06.18 |