풀이
[문제 풀이]
처음에 이 문제를 풀었을 때, 단순히 크루스칼 알고리즘으로 풀었다.
외계신들 간의 거리만 계산해 priority_queue에 넣으면 매우 쉽게 풀 수 있기 때문이다.
문제는 크루스칼 알고리즘이나 heap을 이용한 prim알고리즘은 시간복잡도가 O(ElogV)인데, 이 문제에서 E=V^2이기 때문에 O(V^2)의 prim알고리즘을 사용하면 더 빨리 문제를 해결할 수 있다.
O(V^2)의 prim알고리즘을 간단히 설명하면
정점은 {현재 방문한 노드}와 {아직 방문하지 않은 노드}의 두 집합으로 나눌 수 있다.
여기서, 현재 방문한 노드들과 아직 방문하지 않는 노드를 연결하는 모든 간선 중 가장 비용이 적게 드는 간선을 추가해 나가는 방법이다.
단순히 글로 보면 방문했던 노드들에서 다른 노드로 가는 비용의 최솟값을 계산해야하기 때문에 시간복잡도가 O(V^2)을 넘어간다고 생각할 수 있지만, memoization을 이용하면 크기가 V인 배열을 이용해 반복을 줄일 수 있다.
아래 그림을 보며 어떻게 작동하는지 알아보자.

1번 정점에서 MST를 그리기 시작하면, 먼저 dist 배열을 갱신한다.
dist 배열이란 특정 정점에 도달하는데 걸리는 비용이다.
이제 비용의 갱신이 끝났으면 아직 방문하지 않은 정점 중에서 비용이 최소인 정점을 찾는다.
위 그림에서는 2번 정점에 도달하는 비용이 가장 적으므로 2번 정점에 방문을 한다.
2번 정점에 방문했으므로 다시 dist를 갱신해야한다.
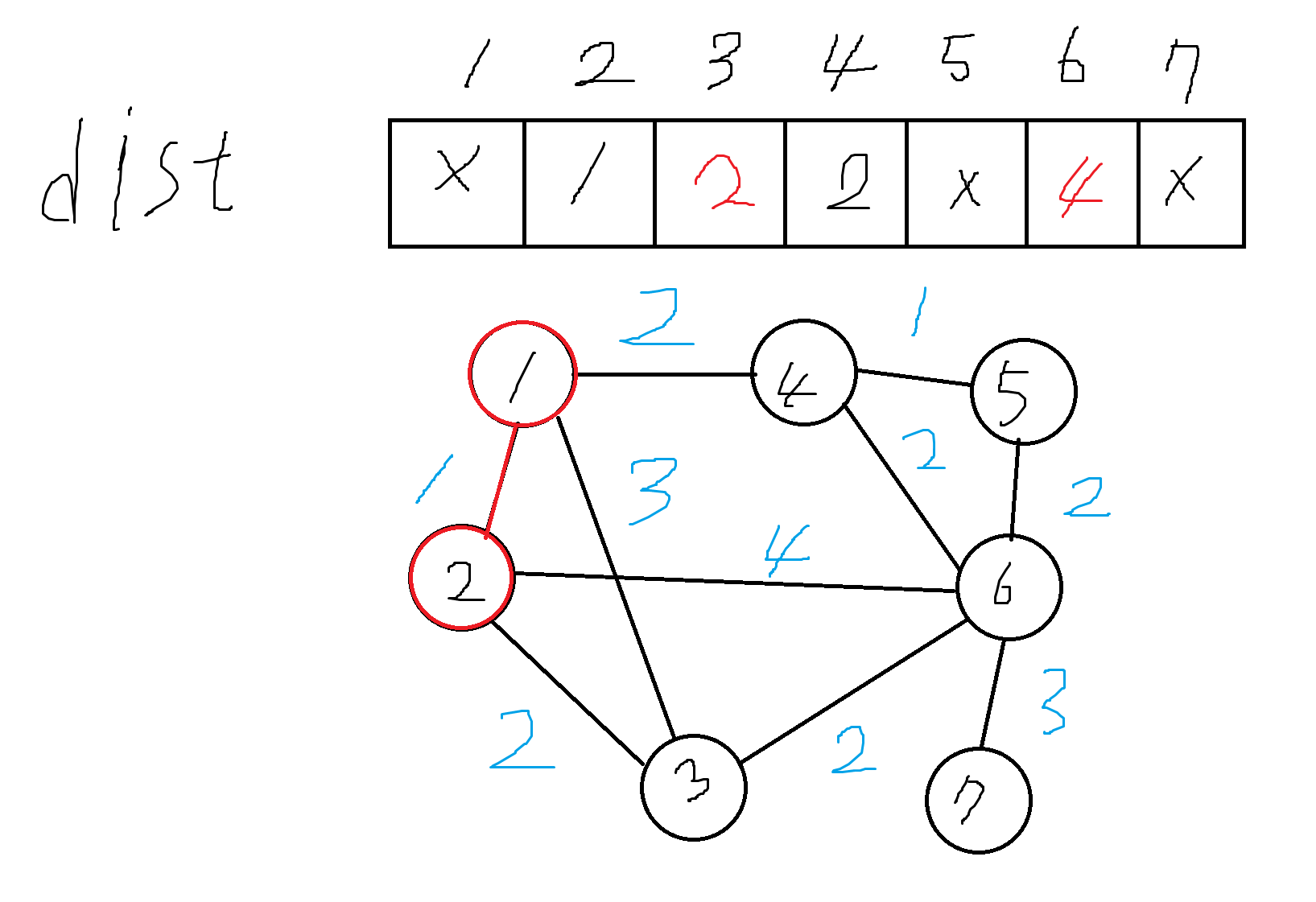
빨간색으로 변한 값이 새로 갱신된 dist의 값이다.
이제 마찬가지로 방문한 적이 없으면서 방문할 수 있는 정점 중 가장 비용이 적게 드는 정점을 선택해 방문하는 과정을 모든 정점에 방문할 때 까지 반복하면 된다.
이후 모든 정점에 방문했다면, MST를 만드는 비용을 출력하면 된다.
[아이디어 정리]
- 외계신 간에 연겷하는데 필요한 비용을 계산한다.
- 비용의 계산이 끝나면 prim알고리즘, 크루스칼 알고리즘 등을 이용해 MST의 비용을 계산한다.
- 계산한 MST의 비용을 출력한다.
Code (Prim O(V^2))
#include <string>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
using namespace std;
struct st {
int st;
int ed;
double cost;
};
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M;
cin >> N >> M;
vector<pair<int, int>> v(N+1);
vector<vector<double>> graph(N+1,vector<double>(N+1, 10000000));
double cost;
int y, x;
vector<bool> visited(N + 1, false);
for (int i = 1; i <= N; i++) { // 1번 우주신 부터 기록해야함 범위가 1~N이므로
cin >> v[i].first >> v[i].second;
for (int j = 1; j < i; j++) {
cost = sqrt(pow(v[i].first - v[j].first, 2) + pow(v[i].second - v[j].second, 2));
graph[i][j] = cost;
graph[j][i] = cost;
}
}
vector<double> dist(N + 1, 10000000);
for (int i = 0; i < M; i++)
{
cin >> y >> x;
graph[y][x] = 0;
graph[x][y] = 0;
}
double answer=0;
int nextN = 1;
for (int i = 1; i < N; i++) {
double minCost = 10000000;
int nowMin = -1;
visited[nextN] = true;
for (int i = 1; i <= N; i++)
{
dist[i] = min(dist[i], graph[nextN][i]);
if (!visited[i] && minCost > dist[i])
{
nowMin = i;
minCost = dist[i];
}
}
answer += minCost;
nextN = nowMin;
}
cout << fixed;
cout.precision(2);
cout << answer;
return 0;
}
Code (크루스칼)
#include <string>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
using namespace std;
struct st {
int st;
int ed;
double cost;
};
struct cmp {
bool operator ()(const st &a, const st &b)const {
return a.cost > b.cost;
}
};
int FindPar(vector<int> &par, int idx)
{
if (par[idx] == idx) {
return idx;
}
return par[idx] = FindPar(par, par[idx]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int N, M;
cin >> N >> M;
vector<pair<int, int>> v(1);
double y, x;
vector<int> par(N+1);
st ST;
priority_queue<st, vector<st>, cmp> q;
for (int i = 1; i <= N; i++) { // 1번 우주신 부터 기록해야함 범위가 1~N이므로
cin >> y >> x;
v.push_back(make_pair(y, x));
par[i] = i;
for (int j = 1; j < i; j++) {
ST.cost = sqrt(pow(y - v[j].first, 2) + pow(x - v[j].second, 2));
ST.st = i;
ST.ed = j;
q.push(ST);
}
}
ST.cost= 0;
for (int i = 0; i < M; i++)
{
cin >> ST.st >> ST.ed;
q.push(ST);
}
double answer = 0;
int a, b;
while (!q.empty()) {
ST = q.top();
q.pop();
a=FindPar(par, ST.st);
b = FindPar(par, ST.ed);
if (a != b) {
par[a] = b;
answer += ST.cost;
}
}
cout << fixed;
cout.precision(2);
cout << answer;
return 0;
}처음에 크루스칼 알고리즘으로 문제를 풀었더니 시간이 약 100ms가 나왔고, 다른 사람들에 비해 매우 느렸다.
그래서 다시 priority_queue를 이용한 prim 알고리즘으로 풀었는데, 그래도 똑같이 시간이 100ms가 나왔다.
(구현한 두 알고리즘의 시간복잡도가 같기 때문에 당연한 일이었다.)
그래서 다른사람의 코드를 봤는데, 단순히 이중 for문으로 문제를 풀었다는 사실을 확인했다.
코드가 어떤 방식으로 작동되는지 이해하고 혹시 MST를 만드는 다른 알고리즘이 있나? 검색을 해봤는데, 아무리 찾아봐도 작동방식이 비슷한 알고리즘이 없었다
나중에 보니 배열을 이용한 pirm 알고리즘이었다...
분명 계속 고민하면서 다익스트라랑 비슷하다고 생각 했으면서 왜 눈치를 못챘을까;;;
아오...
https://www.acmicpc.net/problem/1774
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 트리와 쿼리 (No. 15681) (1) | 2024.06.03 |
|---|---|
| [백준/C++] 전력난 (No. 6497) (1) | 2024.06.02 |
| [백준/C++] 다리 만들기 2 (0) | 2024.05.31 |
| [백준/C++] 별자리 만들기 (No. 4386) (1) | 2024.05.30 |
| [백준/C++] 최소 스패닝 트리 (0) | 2024.05.30 |