풀이
[문제 풀이]
이 문제는 규칙만 잘 생각하면 쉽게 풀 수 있는 문제다.
N과 K가 주어지면 N은 K로 나누어 떨어진다.
이때, N/K개의 팀을 나누고, 각 팀의 전투력의 합이 K로 전부 나누어떨어지지 않게 만들 수 있는지 구하는 문제다.
가장 먼저 생각할 수 있는 경우는 K가 1인 경우다.
K가 1이라면, 모든 팀은 K로 나누어떨어지기 때문에 당연히 정답은 "NO"다.
이제 K가 1 이상일 경우를 생각해보자.
가장 쉬운 방법은 1 ~ N의 전투력을 가진 사람을 K명씩 나누어 팀을 만들기 때문에, 각 팀에 전투력을 K로 나누었을 때 나머지가 1, 2, ... , k-1, 0 인 사람으로 채우는 것이다.

이제 위와 같이 각 팀의 인원을 고르게 채웠으므로, 나머지의 합을 더해 K로 나누어 떨어지는지 검사한다.
각 팀의 나머지의 합은 K*(K-1)/2로 쉽게 구할 수 있다.
그러므로 K*(K-1)/2를 K로 나누었을 때, 나머지가 0이 아니라면 각 팀에 전투력을 K로 나눈 나머지가 0 ~ K-1인 사람을 한명 씩 두면 조건에 맞게 팀을 만들 수 있다.
이제 다음으로 고려할 경우는 K*(K-1)/2를 K로 나눈 나머지가 0인 경우다. 이 경우는 적절히 팀에 인원을 분배해 주어야 한다.
+ 여기서 K*(K-1)/2를 K로 나눈 나머지가 0인데, N과 K가 같다면 1팀밖에 존재하지 않으므로 조건에 맞게 배치할 수 없는 경우이므로 "NO"를 출력하면 된다.
이제 N과 K가 다른 경우에 어떻게 인원을 분배해야할 지 고민해 보자.
분배하는 방법은 쉽다.
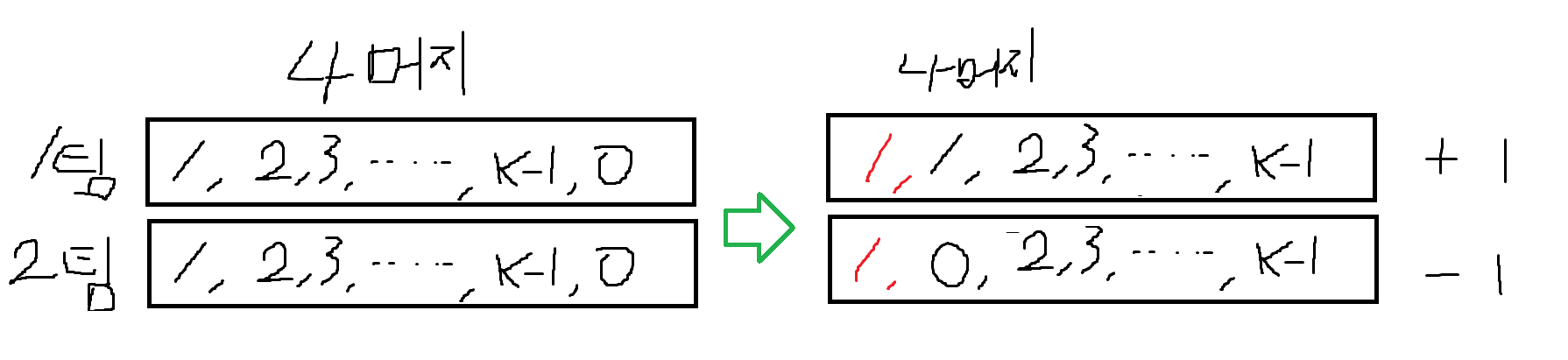
1팀의 나머지가 1인 사람을 2팀으로 보내고 2팀의 나머지가 0인 사람을 1팀으로 보내면 쉽게 해결된다.
왜냐하면 a=K*(K-1)/2라고 했을 때, 1팀의 나머지 합은 a+1, 2팀의 나머지 합은 a-1로 나타낼 수 있다.
이때, a가 K로 나누어 떨어졌고, K는 1이 아니므로 a+1을 K로 나누면 나머지가 1로 나누어 떨어지지 않는다.
마찬가지로 a-1을 K로 나누면 나머지는 K-1로 나누어 떨어지지 않게 된다.
이렇게 두 팀의 인원을 한명만 바꿔주는것으로 쉽게 문제를 해결할 수 있다.
이제 마지막으로 고려해야할 예외 케이스다.
위의 방법은 2팀의 인원을 바꿔 주는 방법이므로, 짝수 팀에 해당하는 방법이다.
팀의 수가 홀수일 경우는 어떻게 해야할까?
팀의 수가 홀수일 경우는 3팀에 인원을 잘 분배해 주고, 나머지 팀은 팀의 수가 짝수일 경우와 같이 해결하면 된다.

위 그림과 같이 3개의 팀의 나머지를 분배해주면 된다.
1팀은 나머지가 1인 인원을 2팀으로 보내고, 2팀은 나머지가 2인 인원을 3팀으로 보낸다.
3팀은 나머지가 0인 인원을 1팀으로 보내면
1팀의 나머지 : a-1
2팀의 나머지 : a-1
3팀의 나머지 : a+2
와 같이 바뀐다.
위 방법에 따르면 K가 1이 아닐 때 a-1의 나머지는 K-1, a+2의 나머지는 2라는 사실을 알 수 있다.
분배를 필요로 하는 나머지 팀들은 수가 짝수이므로 나머지를 +1, -1 하는 방법으로 해결이 됨을 알 수 있다.
+ 여기서 나머지가 a+2인 팀의 경우 K가 2라면 불가능한 경우지 않을까? 라는 생각이 들 수 있다.
하지만 K가 2인 경우 각 팀은 K*(K-1)/2의 값이 1로 애초에 분배가 필요한 경우에 해당하지 않는다.
그러므로 위 방법으로 모든 경우를 조건에 맞게 해결할 수 있다.
[아이디어 정리]
- K가 1인 경우는 항상 정답이 "NO"다.
- K가 1이 아니라면 N/K개의 팀에 전투력을 K로 나눈 값이 [0,1,2, ... , K-1]이 되도록 인원을 배치한다.
- 고르게 인원을 배치했다면 나머지의 합을 구한다. (나머지의 합(a) = K*(K-1)/2)
- 만약 나머지의 합 a를 K로 나누었을 경우 나머지가 0이 아니라면, 이대로 배치하면 되므로 "YES"를 출력하고 번호를 출력한다.
- 만약 나머지의 합 a를 K로 나누었을 경우 나머지가 0이라면, 팀의 수가 1인지 검사한다. (N과 K가 같은지)
- 팀의 수가 1이라면 "NO"를 출력한고, 아니라면 "YES"를 출력한다.
- 팀의 수가 짝수라면, 두 팀의 인원을 한 명만 변경해 두 팀의 나머지 합을 -1, 1로 만들어 해결할 수 있다.
- 팀의 수가 홀수라면, 세 팀의 인원을 한 명씩 변경해 세 팀의 나머지 합을 [-1, -1, 2]로 만들어 해결할 수 있다. (이후 나머지 팀들은 7번 방법으로 해결할 수 있기 때문)
Code
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL),cout.tie(NULL);
long long N, K;
cin >> N >> K;
if (K == 1) { // K가 1인경우
cout << "NO";
return 0;
}
long long t = K * (K - 1) / 2;
if (t % K != 0) { // K*(K-1)/2를 K로 나누었을 때 0이 아닌 경우
cout << "YES\n";
for (int i = 0; i < N / K; i++) {
for (int j = 1; j <= K; j++) {
cout << i * K + j << " ";
}
cout << "\n";
}
}
else
{
if (N/K==1) // 팀이 1팀이며 나머지 합이 K로 나누어 떨어지는 경우
{
cout << "NO";
}
else
{
int cs = N / K;
if (cs % 2 == 0) // 팀의 수가 짝수인 경우
{
cout << "YES\n";
for (int i = 0; i < cs; i+=2) {
for (int j = 2; j <= K; j++) {
cout << i * K + j << " ";
}
cout << (i + 1) * K + K<<"\n";
cout << i * K + 1 << " ";
for (int j = 1; j < K; j++) {
cout << (i + 1) * K + j << " ";
}
cout << "\n";
}
}
else //팀의 수가 홀수인 경우
{
// 3팀의 인원을 분배하는 방법
cout << "YES\n";
// 0,0,2,3, 1,1,0,3, 1,2,2,3
for (int j = 2; j <= K; j++) {
cout << j << " ";
}
cout << 3*K << "\n";
cout << 1 << " ";
cout << K + 1 << " ";
for (int j = 3; j <=K; j++) {
cout << K + j << " ";
}
cout << "\n";
for (int j = 1; j < K; j++) {
cout << K*2 + j << " ";
}
cout << K + 2 << "\n";
// 아래는 팀의 수가 짝수인 경우의 인원 분배 방법
for (int i = 3; i < cs; i += 2) {
for (int j = 2; j <= K; j++) {
cout << i * K + j << " ";
}
cout << (i + 1) * K + K << "\n";
cout << i * K + 1 << " ";
for (int j = 1; j < K; j++) {
cout << (i + 1) * K + j << " ";
}
cout << "\n";
}
}
}
}
return 0;
}
아이디어는 떠올랐는데, 논리적으로 옳다고 판단하는데 시간이 좀 걸렸고 K가 1인 경우를 제외해서 바로 안풀렸다.
심지어 나머지 합인 K*(K-1)/2를 int형으로 나누어 나머지를 구해버려서 int형 범위를 초과하는 부분에서 오류가 생겼었다... 매번 변수형 조심하자!
https://www.acmicpc.net/problem/31873
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/C++] 집합의 표현 (No. 1717) (0) | 2024.05.24 |
|---|---|
| [백준/C++] 트리 (0) | 2024.05.23 |
| [백준/C++] 이진 검색 트리 (0) | 2024.05.22 |
| [백준/C++] 트리의 순회 (0) | 2024.05.20 |
| [백준/C++] 트리 순회 (0) | 2024.05.17 |