문제
https://www.acmicpc.net/problem/17136
<그림 1>과 같이 정사각형 모양을 한 다섯 종류의 색종이가 있다. 색종이의 크기는 1×1, 2×2, 3×3, 4×4, 5×5로 총 다섯 종류가 있으며, 각 종류의 색종이는 5개씩 가지고 있다.
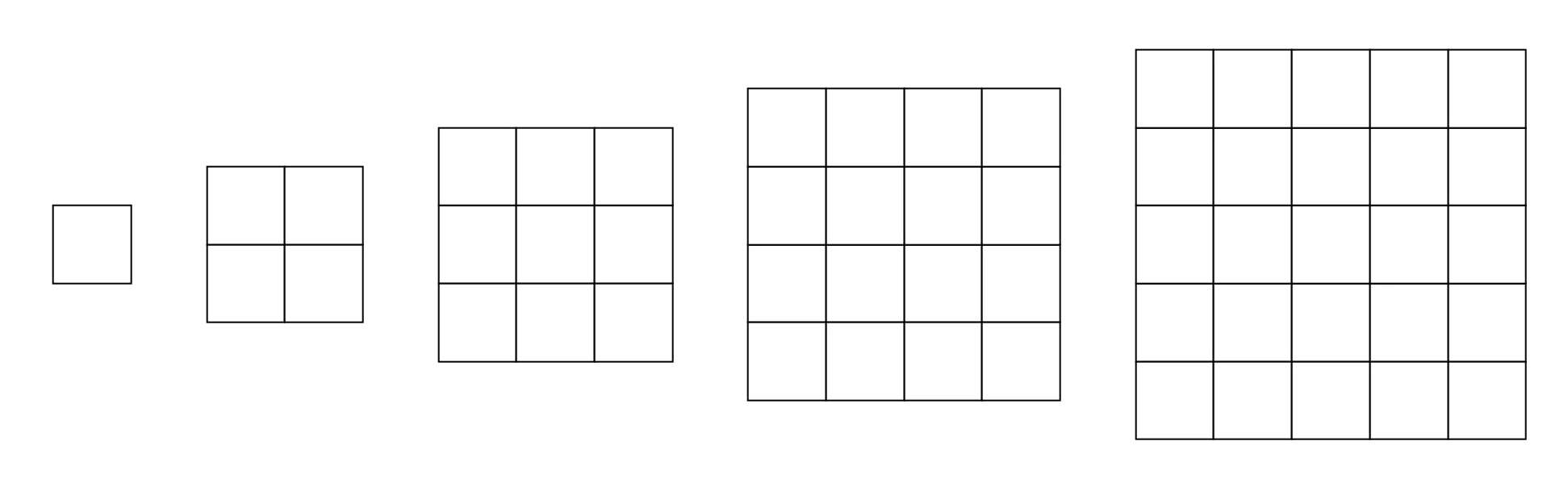
색종이를 크기가 10×10인 종이 위에 붙이려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 0 또는 1이 적혀 있다. 1이 적힌 칸은 모두 색종이로 덮여져야 한다. 색종이를 붙일 때는 종이의 경계 밖으로 나가서는 안되고, 겹쳐도 안 된다. 또, 칸의 경계와 일치하게 붙여야 한다. 0이 적힌 칸에는 색종이가 있으면 안 된다.
종이가 주어졌을 때, 1이 적힌 모든 칸을 붙이는데 필요한 색종이의 최소 개수를 구해보자.
입력
총 10개의 줄에 종이의 각 칸에 적힌 수가 주어진다.
출력
모든 1을 덮는데 필요한 색종이의 최소 개수를 출력한다. 1을 모두 덮는 것이 불가능한 경우에는 -1을 출력한다.
풀이
처음에는 크기가 큰 색종이를 붙여서 풀면 될 줄 알았다. 하지만 색종이의 개수에 제한이 있기 때문에 작은 색종이를 붙여야 해결되는 경우들이 존재했다.
그래서 10x10의 종이 위에 1이 존재할 때 주변 범위를 탐색해 1~5크기의 색종이를 붙이는 경우, 붙이지 않는 경우로 탐색을 했다.
Code
def color(x,y,N,cnt): #
global n_min # 가장 작은 경우의 수 저장
global now # 색종이의 1을 전부 가릴수 있는지 판별
if N==0:
if n_min>cnt:
n_min=cnt
now=True
return
if x>=10: # x방향 범위를 벗어나면 다음 칸으로 이동
color(0,y+1,N,cnt)
return
if y>=10: # y방향 범위를 벗어나면 함수 종료
return
if lst[y][x]:
for n in range(4,-1,-1): #5칸짜리 색종이부터 1칸짜리까지 실행
if paper[n]<5: #n+1칸짜리 색종이의 갯수가 5개가 아니라면
if x+n<10 and y+n<10: #붙인 색종이가 10x10의 범위안에 있다면
num=True
for i in range(n+1):
for j in range(n+1):
if not lst[y+i][x+j]: #(n+1)x(n+1) 색종이를 붙일 수 있는지 판단
num=False
if num: #(n+1)x(n+1) 색종이를 붙일 수 있다면
for i in range(n+1):
for j in range(n+1):
lst[y+i][x+j]=0
a=(n+1)**2
N-=a
cnt+=1
paper[n]+=1
color(x+n+1,y,N,cnt) #색종이를 붙이고 다음 경우의 수를 실행
for i in range(n+1): #색종이를 붙이지 않고 다음 경우의 수를 실행
for j in range(n+1):
lst[y+i][x+j]=1
N+=a
cnt-=1
paper[n]-=1
else:
color(x+1,y,N,cnt) # 종이 위에 칸이 1이 아니라면 다음 칸으로 이동
lst=[list(map(int,input().split())) for _ in range(10)]
paper=[0]*5
n_min=26
N=0
now=False
for i in lst:
N+=i.count(1)
color(0,0,N,0)
if now:
print(n_min)
else:
print(-1)
예전에는 내가 생각한 방법으로 문제를 풀어도 될지 안될지 판단이 잘 안서서, 문제를 풀 때 생각이 많고 오래 걸렸던 것 같다.지금 보면 완전 탐색 문제였네...
반응형
'Algorithm > BAEKJOON' 카테고리의 다른 글
| [백준/Python] 2981번 - 검문 (0) | 2024.01.02 |
|---|---|
| [백준/Python] 17070번 - 파이프 옮기기1 (1) | 2024.01.02 |
| [백준/Python] 2566번 - 최대값 (0) | 2024.01.02 |
| [백준/Python] 18870번 - 좌표 압축 (3) | 2024.01.02 |
| [백준/Python] 2292번 - 벌집 (1) | 2024.01.02 |