풀이
[문제 풀이]
이 문제에서 중요한 점은 순서를 지켜서 방문하는 order의 제약사항에 있다.
order에서 주어지는 데이터를 [선 방문할 방 : 후 방문할 방] 라고 하자
제약사항을 읽어보면 order에 한번이라도 나온 방인 경우 order의 다른 데이터에 나오지 않는다.
즉, 요약하면 하나의 방은
- 먼저 방문할 방
- 나중에 방문할 방
- 상관 없는 방
3가지 경우로 구분할 수 있다.
여기서 먼저 방문할 방이나 상관 없는 방은 언제 방문해도 상관이 없다.
중요한 방은 나중에 방문할 방이다.
나중에 방문해야하는 방은, 사전에 방문해야 하는 방이 있다는 뜻이므로 사전에 방문 해야하는 방을 먼저 방문하면 된다.
그림을 통해 더 쉽게 알아보자.
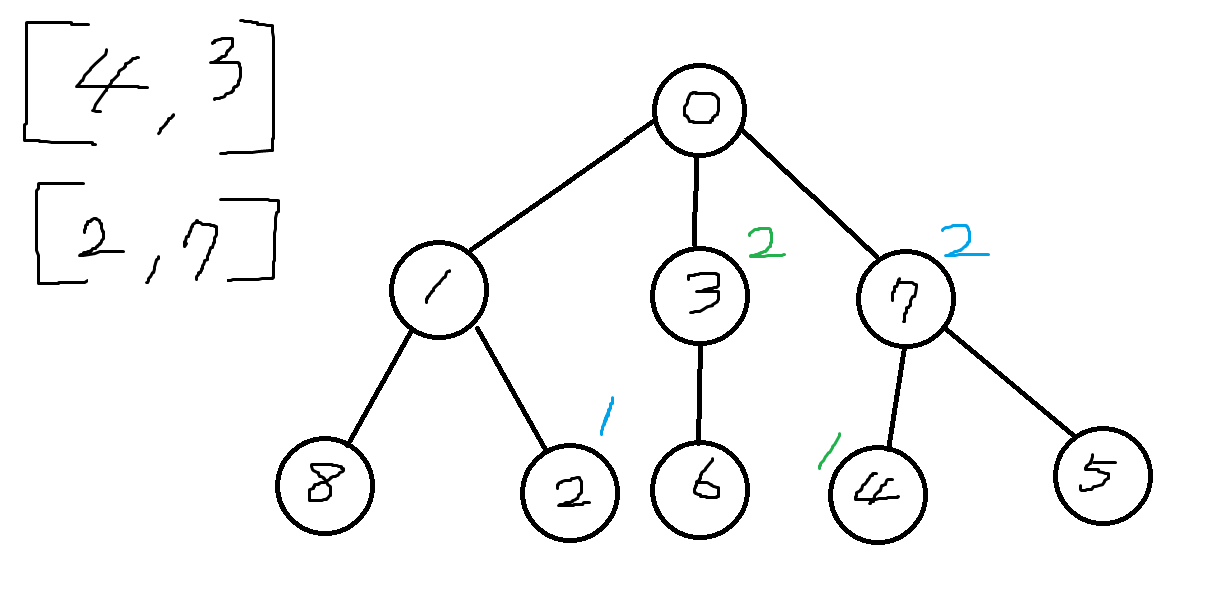
order이 [[4, 3], [1, 7]]으로 주어졌다고 생각해 보자
(여기서 방 옆에 쓰여져있는 숫자 1은 선 방문할 방, 2는 나중에 방문할 방을 의미한다.)
처음에 3번 방을 방문하기 전에 4번 방을 방문해야 하므로 0번에서 시작해 4번 방을 찾아 이동한다.
4번 방으로 이동하는 과정에서 7번 방을 방문하게 되는데, 7번 방은 위에서 말한 3가지 경우 중 2번 경우로 나중에 방문할 방이다.
그러므로 7번방은 사전에 방문해야 하는 방이 있으므로, 그 방을 먼저 방문해야한다.
7번 방에 방문하기 전에 방문해야하는 방은 2번 방이다.
다시 0번 노드에서 2번 방을 찾으러 출발하면 1번 방은 나중에 방문해야 할 방이 아니므로 그냥 방문해도 상관이 없다.
2번방에 방문을 완료했다면, 7번방에 방문할 수 있으므로 7번 방을 방문하고 4번 방을 방문한다.
이후에 3번 방을 방문하면, 나머지 8, 6, 5번 방은 순서에 상관없이 방문할 수 있으므로 모든 방을 방문할 수 있게 된다.
즉, 요약하면 order에서 먼저 방문해야하는 방들을 먼저 방문한다.
만약 그 경로에 나중에 방문해야할 방 A가 있다면, A보다 먼저 방문해야하는 방 B를 먼저 방문하도록 재귀적으로 탐색하면 된다.
이번에는 다른 경우를 살펴보자

order의 데이터가 [[4, 1], [2, 7]] 과 같이 주어졌을 경우
4번 방을 방문하기 위해 0번 노드에서 탐색을 시작한다.
4번 방을 방문하는 경로에 나중에 방문해야하는 방인 7번 방이 있으므로, 7번 방을 방문하기 전에 방문해야 하는 방인 2번 방을 먼저 방문해야한다.
2번 방을 찾으러 가는 경로에 나중에 방문해야하는 방인 1번 방이 있으므로, 다시 1번 방을 방문하기 전에 방문해야 하는 방인 4번 방을 먼저 방문해야 한다.
마찬가지로 다시 4번 방으로 이동하다 보면 7번 방이 나오는 루프가 생기게 된다.
즉, 이렇게 루프가 생기면 조건에 따라 모든 방을 탐색하는 게 불가능하다.
그러므로 Set이나 vector를 이용해 현재 방문하려는 방들이 이전 재귀에 들어있는지 확인하고,
만약 들어있다면 루프인 상태이므로 false를 return하면 된다.
이 방법을 따라 코드를 구현하면 해결 되는 문제다.
[아이디어 정리]
- 먼저 방문해야 하는 방들을 전부 방문하면, 다른 방들은 언제 방문해도 상관이 없다.
- 먼저 방문해야 하는 방들을 전부 방문하는데, 그 경로에 나중에 방문해야할 방 A가 있다면, A보다 먼저 방문해야하는 방 B를 먼저 방문한다.
- B방을 루프가 없이 방문이 가능하면 A방을 방문할 수 있으므로, 탐색을 계속 진행한다.
- 만약 루프가 생긴다면 이 경우에 조건에 따라 모든 방을 방문하는 것은 불가능 하므로, false를 return 한다.
+ 문제 풀이 설명은 0번 부터 탐색을 시작하는 방법을 설명했다.
그러므로 0번 노드에서 BFS나 DFS로 방들을 탐색해 나가면서 나중에 방문해야 하는 방이 나온다면, 그 방보다 먼저 방문해야 하는 방을 기준으로 BFS나 DFS를 수행하도록 코드를 구현하면 된다.
하지만 아래 첨부된 코드는 다른 방법으로 풀어져 있다.
설명하자면 역으로 먼저 방문해야 하는 방에서 0번으로 이동하도록 코드를 구현했고, 그 과정에서 이미 방문한 방이였다면, 코드를 종료하고 루프가 생겼다면 false를 return하도록 했다.
설명은 0번에서 탐색을 시작하는 방법이고, 코드는 역으로 먼저 방문해야 하는 방에서 0번 노드로 도착하는 방법이다.
탐색 방법의 차이라고 생각하면 된다.

왼쪽이 설명한 방법이라면, 실제로 문제를 풀었을 때는 오른쪽과 같이 탐색을 하도록 코드를 구현했다..
(빨간 화살표가 탐색 방향을 의미)
Code
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <iostream>
using namespace std;
// 부모노드, 방문처리, 현재노드,
// 선방문:후방문, 나중에 방문해야하는 노드Set, 재귀과정에 이미 들어있는지 체크할 Set
bool DFS(vector<int> &parents, vector<bool> &visited, int nowNode,
map<int,int> &nextPrev,set<int> &nextSet, set<int> &roofSet)
{ // 이미 방문한 노드가 나올 때 까지의 경로에 나중에 방문해야하는 노드가 있는지 검사한다.
// 만약 나중에 방문해야하는 노드가 있다면, 그 노드의 선 방문 노드를 먼저 방문한다.
int tempNode=nowNode;
if (roofSet.find(nowNode)!=roofSet.end()) //루프가 있으면 불가능 한 경우
{
return false;
}
roofSet.insert(nowNode);
queue<int> visitedQ;
while(!visited[tempNode])
{
if (nextSet.find(tempNode)!=nextSet.end()) // 후 방문 노드라면
{
bool flag = DFS(parents, visited, nextPrev[tempNode], nextPrev,nextSet,roofSet);
if (!flag)
{
return flag;
}
}
visitedQ.push(tempNode);
if (tempNode==0)
{
break;
}
tempNode=parents[tempNode];
}
while(!visitedQ.empty())
{
if (!visited[visitedQ.front()])
visited[visitedQ.front()]=true;
else
break;
visitedQ.pop();
}
return true;
}
bool solution(int n, vector<vector<int>> path, vector<vector<int>> order) {
bool answer = true;
vector<int>parents(n);
vector<vector<int>> nodePath(n);
for (int i=0; i<path.size(); i++)
{
nodePath[path[i][0]].push_back(path[i][1]);
nodePath[path[i][1]].push_back(path[i][0]);
}
queue<int> q;
q.push(0);
while (!q.empty())
{
int nowN=q.front();
q.pop();
for (int i=0; i<nodePath[nowN].size(); i++)
{
if (nodePath[nowN][i]!=parents[nowN])
{
parents[nodePath[nowN][i]]=nowN;
q.push(nodePath[nowN][i]);
}
}
}
map<int,int> nextPrev; // 후방문:선방문
set<int> nextSet;
for (int i=0; i<order.size(); i++)
{
nextPrev[order[i][1]]=order[i][0];
nextSet.insert(order[i][1]);
}
vector<bool> visited(n,false);
for (int i=0; i<order.size(); i++)
{
if (!visited[order[i][0]])
{
set<int>roofSet;
bool fff=DFS(parents, visited, order[i][0], nextPrev,nextSet, roofSet);
if (!fff)
{
return fff;
}
}
}
return answer;
}
처음에 먼저 방문해야하는 방들을 전부 방문하면 나머지 방들은 탐색할 필요가 없다는 생각이 들어 탐색을 0번 방이 아니라 order의 먼저 방문해야하는 방들을 기준으로 시작했다.
이 과정에서 DFS를 역으로 시작했더니 약간 헷갈렸다...
방문 처리를 하는 과정에서 예외케이스도 생겨서 문제를 푸는데 시간이 오래 걸릴뻔 했다;;
그래도 깔끔하게 풀 수 있는 문제였다.
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] 고고학 최고의 발견 (2) | 2024.03.23 |
|---|---|
| [프로그래머스/C++] 선입 선출 스케줄링 (0) | 2024.03.21 |
| [프로그래머스/C++] 인사고과 (1) | 2024.03.19 |
| [프로그래머스/C++] 매칭 점수 (2019 KAKAO BLIND RECRUITMENT) (4) | 2024.03.18 |
| [프로그래머스/C++] 호텔 방 배정 (3) | 2024.03.16 |