풀이
[문제 풀이]
이 문제는 풀면서 고민을 많이 했던 문제다.
n의 범위가 250000 이기 때문에 2차원 vector로 거리를 저장 하기에는 무리였다. 그렇다고 하나의 노드가 들어올 때 마다 노드들의 거리를 측정해 계산하자니, 약 250000*250000이기 때문에 이것도 무리라는 생각이 들었다.
그래서 노드들의 관계가 트리로 주어지기 때문에 하나의 노드를 부모 노드로 지정하고, 반복해서 자식 노드들을 잘 탐색하면 문제가 풀리지 않을까? 라는 생각을 했다.
여기서 먼저 짚고 가야하는 점이 있다.
f(a, b, c)를 구할 때, 중간값을 가장 크게 하려면 어떻게 해야할까?
정답은 가장 거리가 긴 노드들을 알면 된다.
예를 들어 특정 노드 a, b의 거리가 가장 멀다고 가정하자.
그러면 이 노드들은 트리 구조를 가지고 있기 때문에 가장 큰 중간 값은 a, b의 거리이거나, a, b거리에 1을 뺀 값이다.
아래 그림을 보면 쉽게 이해가 된다.
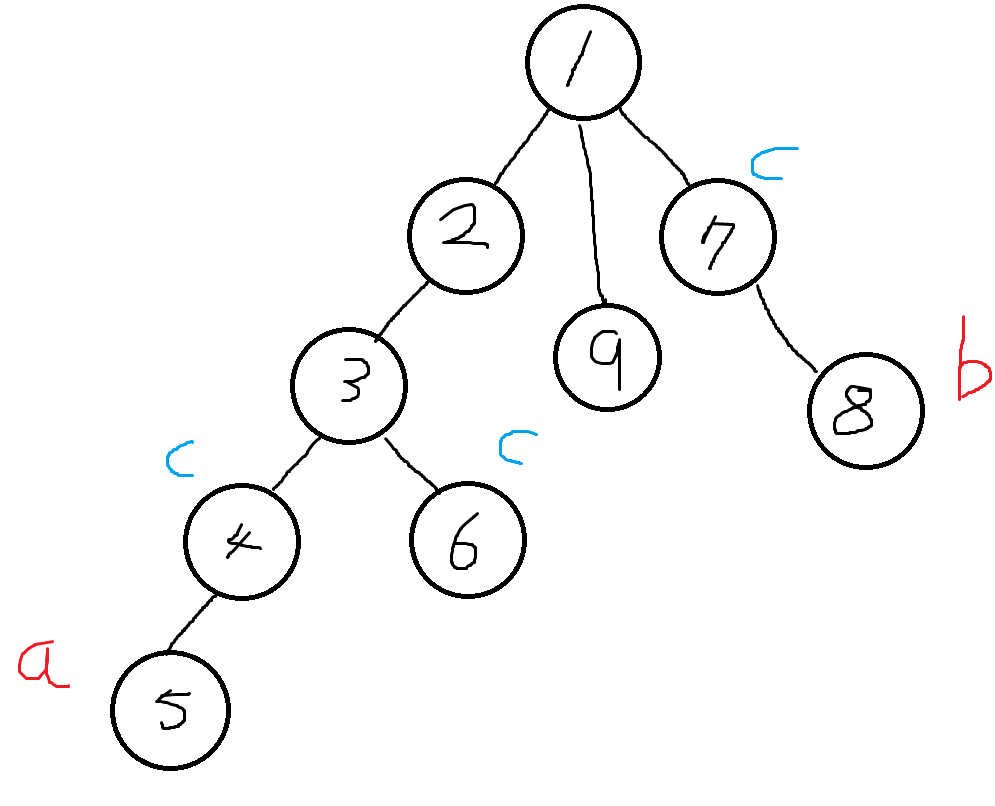
그림에서 볼 수 있듯이, 트리 구조이기 때문에 a, b노드에는 부모노드가 존재할 것이고, 중간 값을 크게 만드는 c는 a나 b의 부모노드이거나, 아예 다른 노드일 수 밖에 없다는 뜻이다.
(구하고 싶은 값이 중간 값의 최대값이기 때문에 나머지 작은 값은 무시해도 된다.)
이제 이 사실을 알았으니 어떻게 하면 가장 거리가 먼 a,b노드를 구할 수 있을지 생각해보자.
그림을 잘 살펴보면 특정 노드를 최상단으로 했기 때문에, 자식 노드들의 깊이를 이용해 특정 노드들간의 거리를 구할 수 있다.
a노드(5번 노드)는 1번 노드로부터 깊이가 4이고, b노드(8번 노드)는 1번 노드로부터 깊이가 2다.
이를 이용하면 a노드와 b노드의 거리는 6으로 나타낼 수 있다.
이제 노드의 거리를 구하기 전에, 주의해야할 점이 있다.

a노드는 깊이가 4이고, c노드는 깊이가 3이다. 그렇다면, a노드와 c노드의 거리는 7일까?
실제로 a노드와 c노드의 거리는 3이다.
a와 c노드의 첫 공통 부모는 3번 노드로 3번 노드를 기준으로 a노드는 깊이가 2, c노드는 깊이가 1이기 때문에 2+1로 a노드와 c노드의 거리는 3임을 알 수 있다.
그러므로 첫 공통 조상이 나오게 되면 노드들의 거리를 계산하고, 그 뒤로는 계산을 하지 않도록 주의를 해야한다.
이제 대략적인 아이디어를 파악했으니 좀 더 자세히 풀이를 생각해 보자.

위 그림에서 가장 큰 중간값은 f(a, b, c)가 아니라 f(a, b, d)다.
만약 문제를 풀 때, 가장 깊은 노드를 하나만 가져간다면 어떻게 될까?
먼저 5번 노드에서 a나 d의 깊이가 1이였으므로, 4번 노드에는 a와 d의 깊이에 1을 더해 2를 return할 것이다.
3번 노드에서는 4번 노드에서 return된 깊이 3과 7번에서 return된 깊이 3을 이용해 a와 b의 깊이 차이 즉, 거리 6을 갖고 있을 것이다.
마지막으로 1번 노드에서 3번 노드로부터 깊이 4, 2번 노드로부터 깊이 1을 return 받아 최종적으로 노드들 간의 거리가 큰 순서로 나열하면 6, 5를 얻게 된다.
하지만 실제로 3번 노드가 부모노드일 때, 6번노드와 9번노드의 거리가 6, 10번노드와 9번 노드의 거리가 6으로 노드들 간의 거리를 내림차순으로 나열하면 6, 6, 5이게 된다. (아래 그림 참고)

그렇기 때문에 놓치는 값이 없도록 항상 노드는 가장 깊은 깊이와 두번째로 깊은 노드의 깊이를 return해 빠지는 경우가 없도록 해야한다.
[예시]
이제 대략적인 아이디어와 주의해야할 점들을 전부 알아봤으니 실제 예를 보며 어떻게 값을 전달해 줄지 알아보자.
아래의 그림에서 1번 노드를 기준으로 탐색을 시작한다.

DFS로 탐색을 하면 6번 노드에 도달하고 6번 노드는 다음과 같은 결과 값을 얻게 된다.
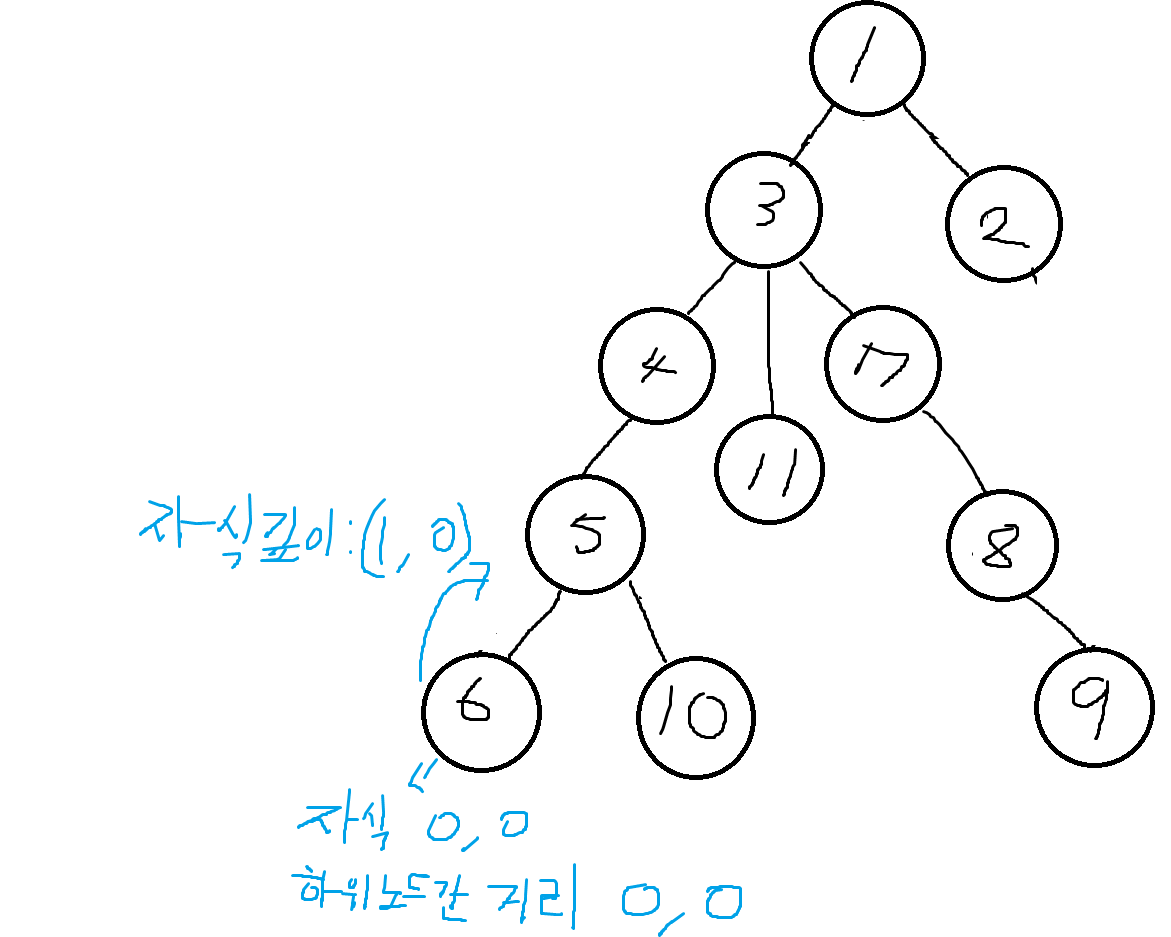
하위 노드가 아예 없으므로 6번을 공통으로 하는 하위 노드 간 거리는 0 이다.
자식노드도 없으므로 자식 중 깊이가 가장 깊은 노드와 그 다음 노드도 0, 0 값이다.
이제 결과 값을 부모노드(5번 노드)에 return해야 하는데, 6번의 자식이 없으므로 5번 노드는 6번으로부터 깊이 1과, 0을 return 받게 된다.
마찬가지로 10번 노드도 6번 노드와 같은 결과 값을 5번 노드에 return하게 된다.
이제 5번 노드는 어떤 값을 4번 노드에 return해줘야 할까?
5번노드 입장에서 가장 깊이가 깊은 노드는 6번과 10번 노드로 1, 1이다.
그러므로 4번 노드에 전달할 때는 깊이인 (2, 2)를 return 해야하고, 이전까지 계산된 하위 노드 간 거리의 최댓값과 그 다음 값을 return하면 된다.
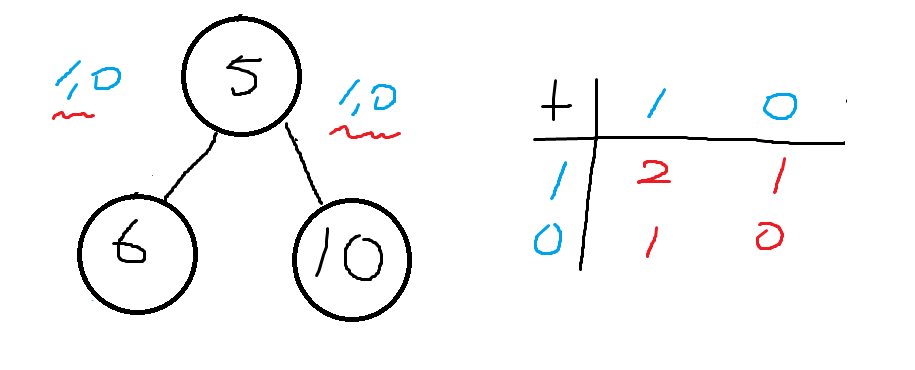
하위 노드간의 거리는 6번과 10번의 깊이를 이용해 구할 수 있다.
6번과 10번의 깊이 1, 1로 구한 거리 2와 다음으로 긴 5번과 (6번 or 10번)의 거리 1을 return하면 된다.
[자식 노드들 깊이: (2, 2), 하위 노드간 거리: (2, 1) ]
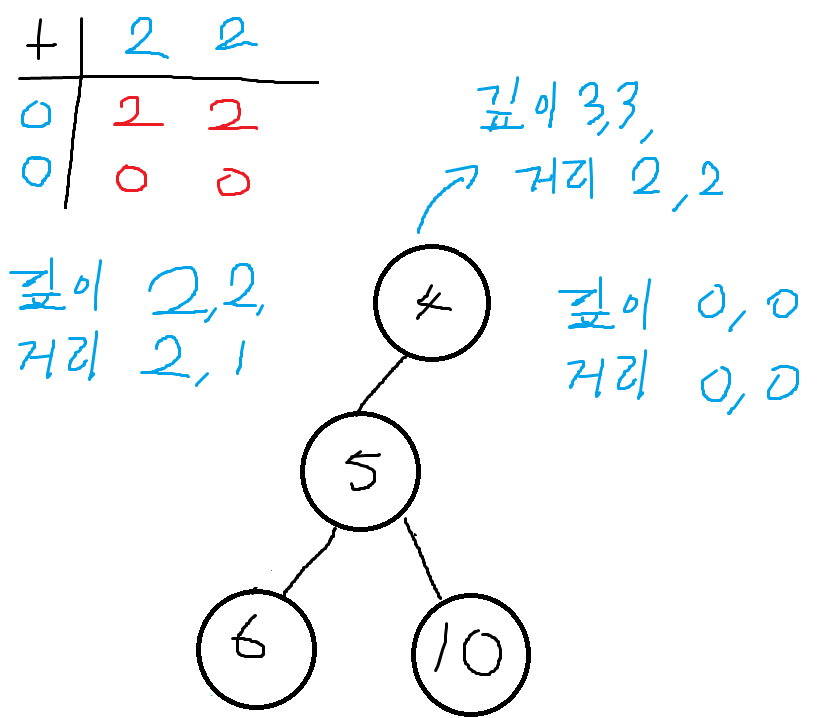
4번 노드는 마찬가지로 5번에서 깊이 (2, 2) 거리 (2, 1)을 받았다.
하지만 다른 자식이 없기 때문에 깊이 (0, 0) 거리 (0, 0)으로 볼 수 있다.
이를 이용하면 다음 부모노드에 깊이 (3, 3) 거리 (2, 2)를 return하게 된다.

3번이 부모노드에 return할 값은 최종적으로, 4번에서 받은 깊이 (3, 3)과 7번에서 받은 깊이 (3, 2)를 이용해 거리 6, 6을 구할 수 있고, 깊이 (4, 4)와 거리 (6, 6)을 return하게 된다.

마지막으로 1번노드는 3번으로 부터 받은 깊이 (4, 4)와 2번으로 부터 받은 깊이 (1, 0)을 이용해 거리를 구하면 5, 5를 구할 수 있다.
하지만 여기서 이전에 3번에서 받은 거리 (6, 6)이 (5, 5) 보다 거리가 더 멀기 때문에 1번은 깊이 (5, 5)와 거리 (6, 6)을 최종적으로 return 하게 된다.
마지막으로 DFS를 마친 1번이 return한 거리 6, 6을 이용하면 가장 긴 노드의 거리는 6이고, 그 다음으로 긴 거리도 6이므로 중간값의 최대값이 6임을 알 수 있다.
설명이 길지만 잘 생각해보면 트리의 성질을 이용해 부등식의 크기 비교와 비슷한 풀이다.
[아이디어 요약]
- 특정 노드를 기준으로 트리를 만든다.
- 특정 노드를 방문 할 때 마다, 자식들 간의 가장 긴 거리와 그 다음으로 긴 거리를 구한다.
- 이를 반복하면서 최종적으로 구한 자식들 간의 거리를 큰 순서로 2개 구해 2번째로 큰 값을 return한다.
Code (sort 이용)
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <algorithm>
using namespace std;
vector<int>parents;
vector<vector<int>>childs;
vector<vector<int>>nodes;
//DFS
vector<int> DFS(int node)
{
vector<int> largeV({0,-1,0,0});
vector<int> newVector;
vector<int> rt34({0,0});
for (int i=0; i<childs[node].size(); i++)
{
newVector=DFS(childs[node][i]);
rt34.push_back(newVector[2]), rt34.push_back(newVector[3]);
rt34.push_back(newVector[0]+largeV[0]);
int t=max(newVector[0]+largeV[1],newVector[1]+largeV[0]);
rt34.push_back(t);
if (largeV[0]<newVector[0])
{
largeV[1]=largeV[0];
largeV[0]=newVector[0];
}
else if (largeV[1]<newVector[0])
{
largeV[1]=newVector[0];
}
if (largeV[1]<newVector[1])
{
largeV[1]=newVector[1];
}
}
sort(rt34.begin(), rt34.end(), [](int a, int b){ return b<a; });
largeV[0]+=1, largeV[1]+=1, largeV[2]=rt34[0],largeV[3]=rt34[1];
return largeV;
}
int solution(int n, vector<vector<int>> edges) {
int answer = 0;
// 특정 점에서 가장 긴 거리, 그 다음으로 긴 거리를 알면 해결할 수 있음
// vector<vector<int>> nodeV(n+1,vector<int>(n+1));
// 특정 노드의 가장 왼쪽 자식, 특정 노드 중 가장 깊은 곳에 있는오른쪽 자식
// 무조건 1번 노드가 최상위 부모다.
parents= vector<int>(n+1,0);
childs=vector<vector<int>>(n+1);
nodes=vector<vector<int>>(n+1);
for (int i=0; i<edges.size(); i++)
{
nodes[edges[i][0]].push_back(edges[i][1]);
nodes[edges[i][1]].push_back(edges[i][0]);
}
queue<int> q;
q.push(1);
while(!q.empty())
{
int nowNode = q.front();
q.pop();
for (int i=0; i<nodes[nowNode].size(); i++)
{
if (nodes[nowNode][i]!=parents[nowNode])
{
childs[nowNode].push_back(nodes[nowNode][i]);
parents[nodes[nowNode][i]]=nowNode;
q.push(nodes[nowNode][i]);
}
}
}
return DFS(1)[3];
}
Code (직접 크기 비교)
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <algorithm>
using namespace std;
vector<int>parents;
vector<vector<int>>childs;
vector<vector<int>>nodes;
//DFS
vector<int> DFS(int node)
{
vector<int> largeV({0,-1,0,0});
vector<int> newVector;
for (int i=0; i<childs[node].size(); i++)
{
newVector=DFS(childs[node][i]);
int t1=max(newVector[3],newVector[0]+largeV[0]);
int t2=max({newVector[2],newVector[0]+largeV[1],newVector[1]+largeV[0]});
if (t2>t1)
{
int t3=t1;
t1=t2;
t2=t3;
}
// 거리 비교
if (largeV[2]<=t1)
{
largeV[3]=largeV[2];
largeV[2]=t1;
}
else if (largeV[3]<t1)
{
largeV[3]=t1;
}
if (largeV[3]<t2)
{
largeV[3]=t2;
}
if (largeV[0]<newVector[0])
{
largeV[1]=largeV[0];
largeV[0]=newVector[0];
}
else if (largeV[1]<newVector[0])
{
largeV[1]=newVector[0];
}
if (largeV[1]<newVector[1])
{
largeV[1]=newVector[1];
}
}
largeV[0]+=1, largeV[1]+=1;
return largeV;
}
int solution(int n, vector<vector<int>> edges) {
int answer = 0;
// 특정 점에서 가장 긴 거리, 그 다음으로 긴 거리를 알면 해결할 수 있음
// vector<vector<int>> nodeV(n+1,vector<int>(n+1));
// 특정 노드의 가장 왼쪽 자식, 특정 노드 중 가장 깊은 곳에 있는오른쪽 자식
// 무조건 1번 노드가 최상위 부모다.
parents= vector<int>(n+1,0);
childs=vector<vector<int>>(n+1);
nodes=vector<vector<int>>(n+1);
for (int i=0; i<edges.size(); i++)
{
nodes[edges[i][0]].push_back(edges[i][1]);
nodes[edges[i][1]].push_back(edges[i][0]);
}
queue<int> q;
q.push(1);
while(!q.empty())
{
int nowNode = q.front();
q.pop();
for (int i=0; i<nodes[nowNode].size(); i++)
{
if (nodes[nowNode][i]!=parents[nowNode])
{
childs[nowNode].push_back(nodes[nowNode][i]);
parents[nodes[nowNode][i]]=nowNode;
q.push(nodes[nowNode][i]);
}
}
}
return DFS(1)[3];
}
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
'Algorithm > 프로그래머스' 카테고리의 다른 글
| [프로그래머스/C++] 110 옮기기 (0) | 2024.02.24 |
|---|---|
| [프로그래머스/C++] 블록 게임 (2019 KAKAO BLIND RECRUITMENT) (0) | 2024.02.23 |
| [프로그래머스/C++] 기둥과 보 설치 (2020 KAKAO BLIND RECRUITMENT) (0) | 2024.02.21 |
| [프로그래머스/C++] 리틀 프렌즈 사천성 (2017 카카오코드 본선) (1) | 2024.02.20 |
| [프로그래머스/C++] 무지의 먹방 라이브 (2019 KAKAO BLIND RECRUITMENT) (1) | 2024.02.19 |