[프로그래머스/C++] 산 모양 타일링 (2024 KAKAO WINTER INTERNSHIP)

 

 

문제

문제 설명

 

 

 

풀이

 

[문제 풀이]

​

이 문제는 이전 삼각형의 개수가 다음 경우의 수에 영향을 미치므로 DP로 풀 수 있다.

 

그림을 그려보면 더 쉽게 점화식으로 표현 할 수 있다.

 

먼저 아래의 그림과 같은 도형이 있을 때, 빨간 부분을 기준으로 경우를 나눌 것이다.

 

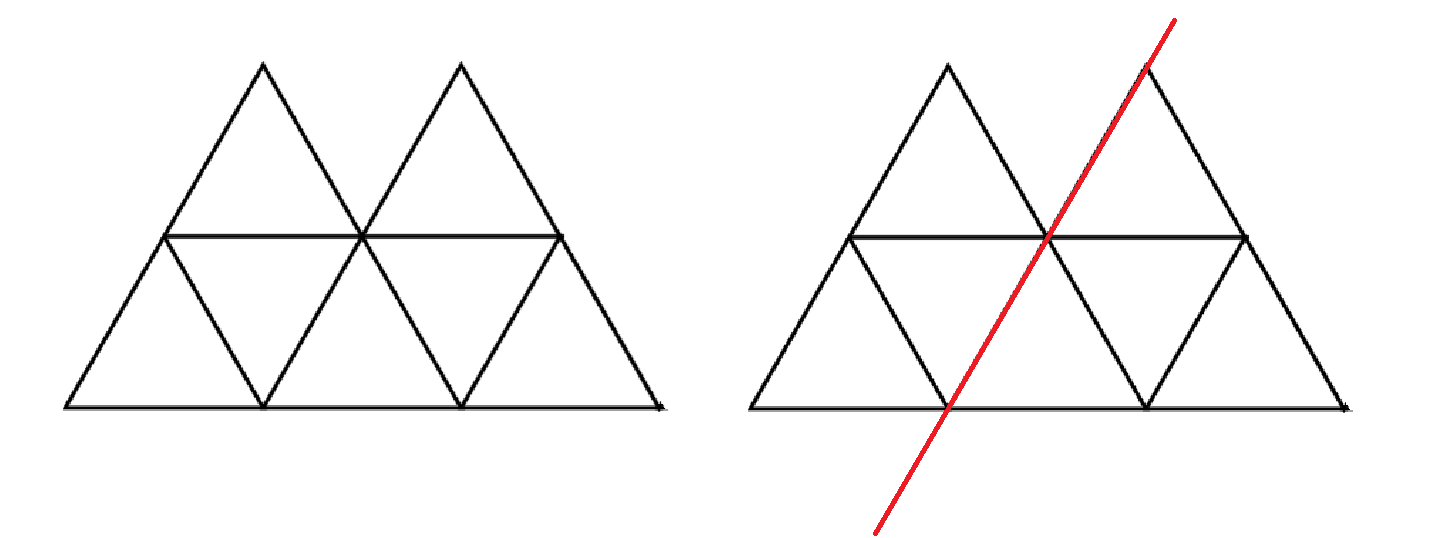
 빨간 선을 기준으로 경우를 나눈 이유는 아래 그림과 같이 마름모가 옆에 있는 삼각형을 침범하는 경우와 침범하지 않는 경우로 나눌 수 있기 때문이다.

그러면 이 마름모를 기준으로 옆 삼각형을 침범하는 경우와 침범하지 않는 경우를 계산해보자

(여기서 빨간색으로 칠해진 삼각형은 2개로 이루어진 마름모형 타일, 파란색 삼각형은 그냥 한개의 삼각형 타일이다.)

 

옆 삼각형을 침범하지 않는 경우  (위쪽에 정삼각형이 있을 때)

 

1. 삼각형이 침범 당하지 않았을 경우 [3가지]

 

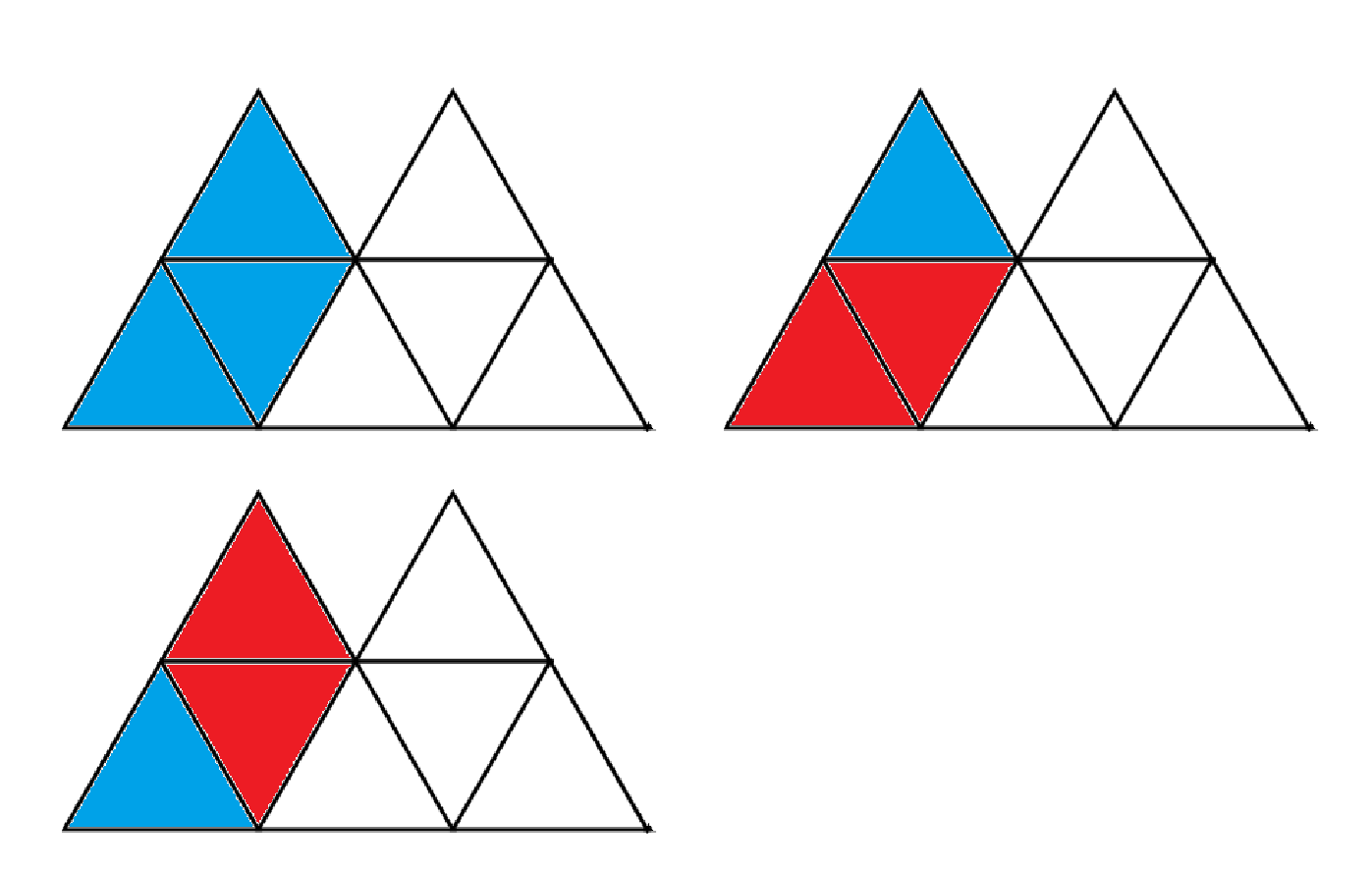
2. 삼각형이 침범 당했을 경우 [2가지]

 

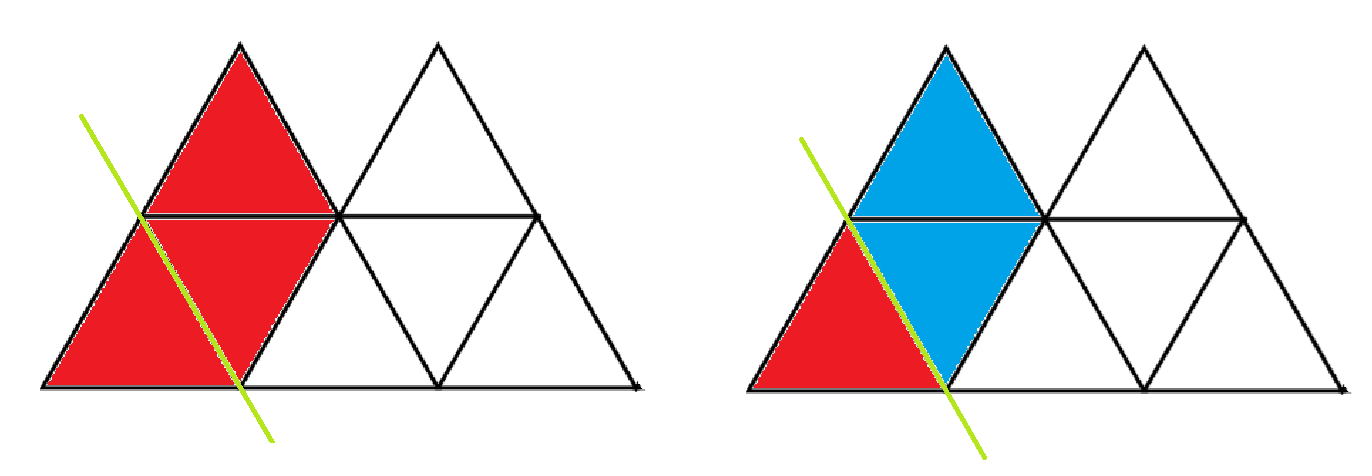
옆 삼각형을 침범하지 않는 경우  (위쪽에 정삼각형이 없을 때)

 

1. 삼각형이 침범 당하지 않았을 경우 [2가지]

 

2. 삼각형이 침범 당했을 경우 [1가지]  

 

 

다음은 옆 삼각형을 침범했을 경우를 생각해보자 이 경우는 매우 쉽게 알 수 있다.

 

위에 삼각형이 있는 경우와 없는 경우가 똑같고, 현재 삼각형이 침범 당한 경우와 침범 당하지 않은 경우를 더한 경우의 수와 같음을 알 수 있다.

 위 그림을 바탕으로 점화식을 세우면

 

 $$\text{옆 삼각형을 침범하지 않는 경우 =   }~ S_n  \text{ ,     옆 삼각형을 침범하는 경우 =   }~ aS_n$$

 $$\text{위에 삼각형이 있을 때,         } ~~~~S_n=3*S_{n-1}+2*aS_{n-1}$$

$$\text{위에 삼각형이 없을 때,       }~~~~ S_n=2*S_{n-1}+aS_{n-1}$$

$$\text{삼각형이 있는 경우와 없는 경우가 동일,     }~~~~ aS_n=S_{n-1}+aS_{n-1}$$

 와 같이 나타낼 수 있다.

 

[아이디어 정리]

1. 옆 삼각형을 침범하는 경우의 마름모를 기준으로 나눈다.
2. 침범했을 경우, 사다리꼴 위에 삼각형이 있는 경우로 경우를 나눠서 점화식을 세운다.
3. 세운 점화식을 바탕으로 경우의 수를 계산하고 10007로 나눈 값을 return한다.

 

 

Code

 

 

#include <string>
#include <vector>
using namespace std;

int solution(int n, vector<int> tops) {
    // 옆 침범 삼각형 aS, 옆 침범x 삼각형 S -> 마지막은 무조건 1짜리다.
    int aS, S,paS,pS;
    paS=0,pS=1;
    for (int i=0; i<tops.size(); i++)
    {
        aS=paS+pS;
        if (tops[i]==1)
        {
            S=pS*3+paS*2;
        }
        else
        {
            S=2*pS+paS;
        }
        paS=aS,pS=S;
        paS%=10007, pS%=10007;
    }
    return (S+aS)%10007;
}

 

---

 

 

처음에 2차원 vector를 만들어서 n-1에 기록 하려고 했는데, 그럴 필요 없이 이전 경우를 저장할 변수만 있으면 되는 문제라 이전 값을 저장할 변수를 선언해서 풀었다.

중간에 답이 틀려서 왜 틀렸는지 이해를 못했는데, 문제에 보니 10007로 나눈 값을 return하라는 조건이 있었다...

 

 

프로그래머스